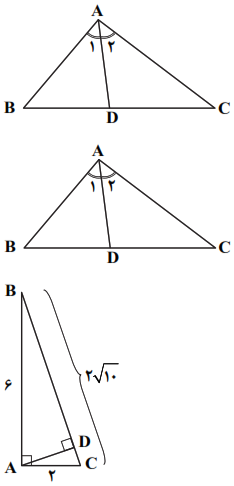
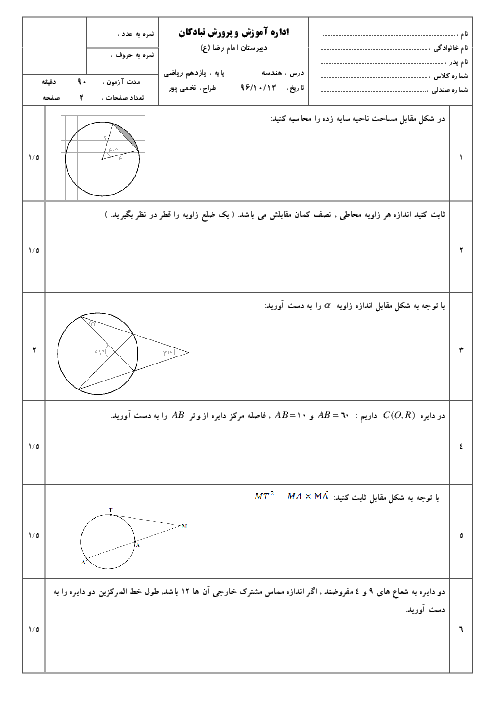
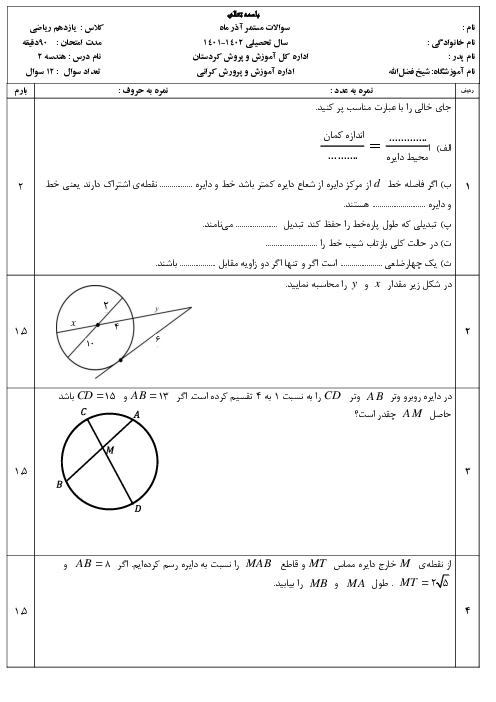
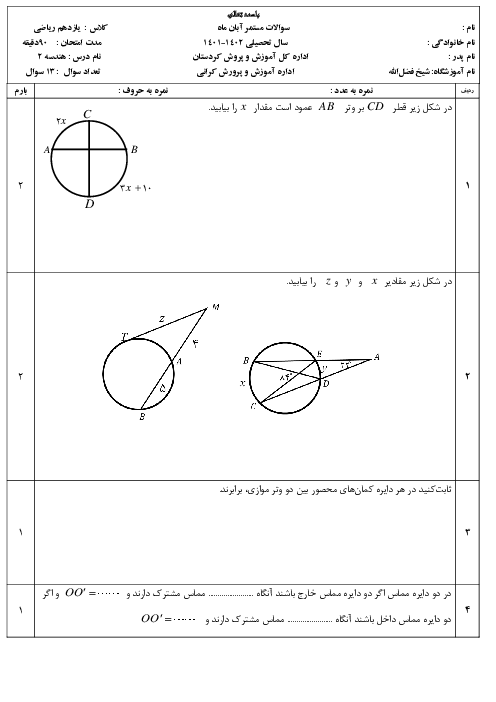
نكته‌ی ۱: بر طبق قضيه‌ی نيمساز زوايای داخلی در مثلث، نيمساز هر زاويه‌ی داخلی، ضلع مقابل را به نسبت اضلاعش تقسيم می‌كند.

${{\hat{A}}_{1}}={{\hat{A}}_{2}}\Rightarrow \frac{AB}{AC}=\frac{BD}{DC}$

نکته‌ی 2: در هر مثلث، مربع نیمساز یک زاویه برابر است با حاصل‌ضرب اندازه‌های دو ضلع منهای حاصل‌ضرب قطعاتی که نیمساز روی ضلع مقابل ایجاد می‌کند.

${{\hat{A}}_{1}}={{\hat{A}}_{2}}\Rightarrow A{{D}^{2}}=AB\times AC-BD\times DC$

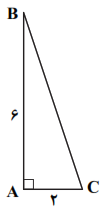
ابتدا به‌کمک قضیه‌ی فیثاغورس، اندازه‌ی وتر BC را به‌دست می‌آوریم:

$BC=\sqrt{4+36}=\sqrt{40}=2\sqrt{10}$

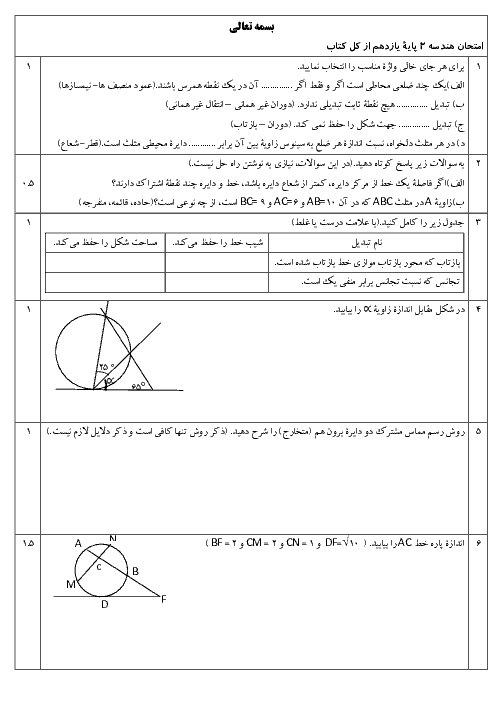
حال با توجه به نکته‌ی 1 و مطابق شکل، طول قطعات BD و DC را به‌دست می‌آوریم:

$\begin{align}
  & \frac{AB}{AC}=\frac{BD}{DC}\Rightarrow \frac{6}{2}=\frac{BD}{2\sqrt{10}-BD}\Rightarrow 6\sqrt{10}-3BD\Rightarrow 4BD\Rightarrow 4BD=6\sqrt{10}\Rightarrow BD=\frac{3\sqrt{10}}{2} \\ 
 & CD=BC-BD=2\sqrt{10}-\frac{3\sqrt{10}}{2}=\frac{\sqrt{10}}{2} \\ 
\end{align}$

و در نهایت با توجه به نکته‌ی 2، اندازه‌ی نیمساز AD، برابر است با:

$A{{D}^{2}}=AB\times AC-BD\times CD=6\times 2-(\frac{3\sqrt{10}}{2})(\frac{\sqrt{10}}{2})=12-\frac{15}{2}=\frac{9}{2}\Rightarrow AD=\frac{3}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$

بنابراین گزینه‌ی 3 پاسخ است.