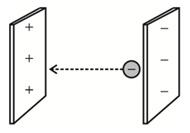
مطابق شكل، الكترونی از مجاورت صفحهٔ با بار منفی خازنی رها می‌شود و با تندی ${{10}^{6}}\frac{m}{s}$ به صفحه مقابل آن میرسد. اگر ظرفيت خازن $16\mu F$ باشد، بار الكتريكی ذخيره شده در اين خازن چند ميكروكولن است؟ (بار و جرم الكترون به‌ترتيب $1/6\times {{10}^{-19}}C$ و $9/1\times {{10}^{-31}}kg$ در نظر گرفته شود و از نيروی وزن وارد بر الكترون صرف‌نظر شود.)
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...