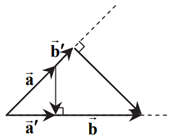
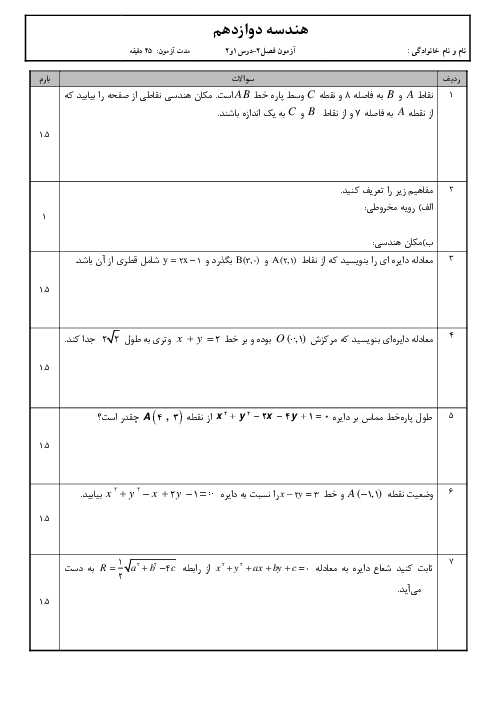
نكته: بردار تصوير قائم $\overrightarrow{a}$ بر امتداد بردار $\overrightarrow{b}$ به‌صورت زیر به‌دست می‌آید:

$\overrightarrow{{{a}'}}=\frac{\overrightarrow{a}.\overrightarrow{b}}{{{\left| \overrightarrow{b} \right|}^{2}}}\overrightarrow{b}$

با توجه به شکل بردار $\overrightarrow{b}-\overrightarrow{{{b}'}}$ بر $\overrightarrow{a}$ عمود است. پس داریم:

$\overrightarrow{a}.(\overrightarrow{b}-\overrightarrow{{{b}'}})=0\Rightarrow \overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{{{b}'}}=0\Rightarrow \overrightarrow{a}.\overrightarrow{b}=\overrightarrow{a}.\overrightarrow{{{b}'}}$

به همین ترتیب بردار $\overrightarrow{a}-\overrightarrow{{{a}'}}$ بر $\overrightarrow{b}$ عمود است: 

$\overrightarrow{b}.(\overrightarrow{{{a}'}}-\overrightarrow{a})=0\Rightarrow \overrightarrow{b}.\overrightarrow{{{a}'}}-\overrightarrow{b}.\overrightarrow{a}=0\Rightarrow \overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{{{a}'}}$

بنابراین:

$\frac{\overrightarrow{a}.\overrightarrow{{{b}'}}+\overrightarrow{b}.\overrightarrow{{{a}'}}}{\overrightarrow{a}.\overrightarrow{b}}=\frac{\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{b}}{\overrightarrow{a}.\overrightarrow{b}}=2$