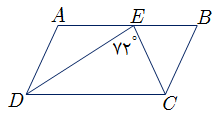
مورب $DE,AB\left\| {DC \Rightarrow {{\hat D}_2} = {{\hat E}_1}} \right.$

مثلث AED متساوی‌الساقین است. پس:

${\hat D_1} = {\hat E_1}$

$\mathop {AED}\limits^\Delta  :\hat A + {\hat E_1} + {\hat D_1} = {180^ \circ }\xrightarrow[{{{\hat E}_1} = {{\hat D}_1}}]{{\hat A = 2x}}2x + {\hat E_1} + {\hat E_1} = {180^ \circ }$

$ \Rightarrow 2{\hat E_1} = {180^ \circ } - 2x \Rightarrow {\hat E_1} = \frac{{{{180}^ \circ } - 2x}}{2} \Rightarrow {\hat E_1} = {90^ \circ } - x$

چهارضلعی AECD یک ذوزنقهٔ متساوی‌الساقین است. پس: ${\hat C_2} = \hat D$

در این چهارضلعی داریم:

$\hat A + ({\hat E_1} + {72^ \circ }) + {\hat C_2} + \hat D = {360^ \circ }$

$\xrightarrow{{{{\hat C}_2} = \hat D}}2x + {\hat E_1} + {72^ \circ } + 2\hat D = {360^ \circ }$

$ \Rightarrow 2x + {\hat E_1} + 2\hat D = {360^ \circ } - {72^ \circ }$

$\xrightarrow{{\hat D = {{180}^ \circ } - \hat A}}2x + {\hat E_1} + 2({180^ \circ } - \hat A) = {288^ \circ }$

$ \Rightarrow 2x + {\hat E_1} + 2({180^ \circ } - 2x) = {288^ \circ }$

$ \Rightarrow 2x + {\hat E_1} + {360^ \circ } - 4x = {288^ \circ }$

${\hat E_1} - 2x = {288^ \circ } - {360^ \circ } =  - 72$

$\xrightarrow{{{{\hat E}_1} = {{90}^ \circ } - x}}{90^ \circ } - x - 2x =  - 72 \Rightarrow  - 3x =  - 72 - 90 =  - 162$

$ \Rightarrow x = \frac{{ - 162}}{{ - 3}} = {54^ \circ }$