يك سكه و يك تاس را پرتاب می‌كنيم. احتمال آن‌كه سكه پشت و تاس زوج بيايد چقدر است؟

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

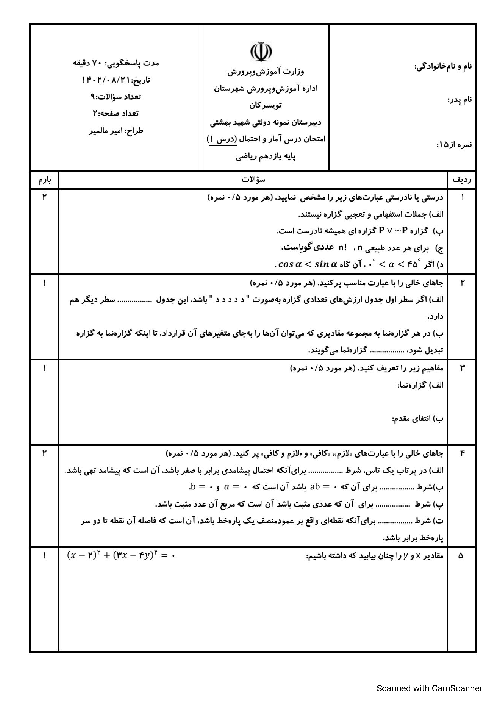
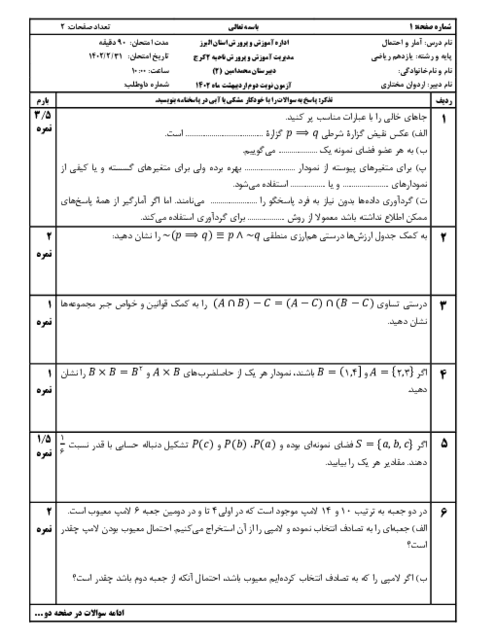
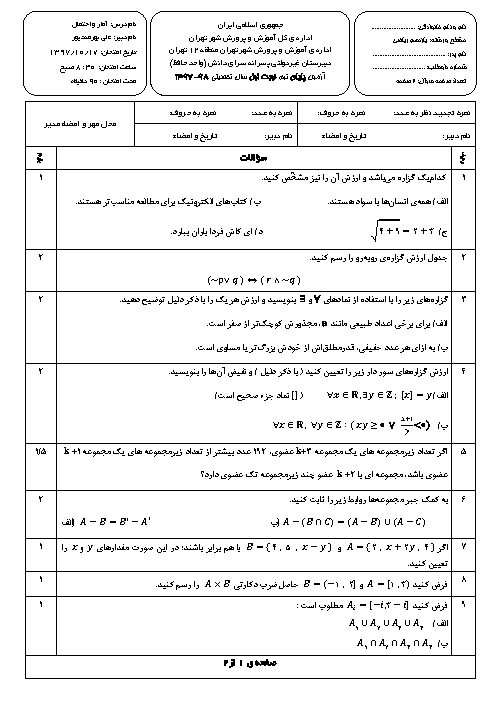
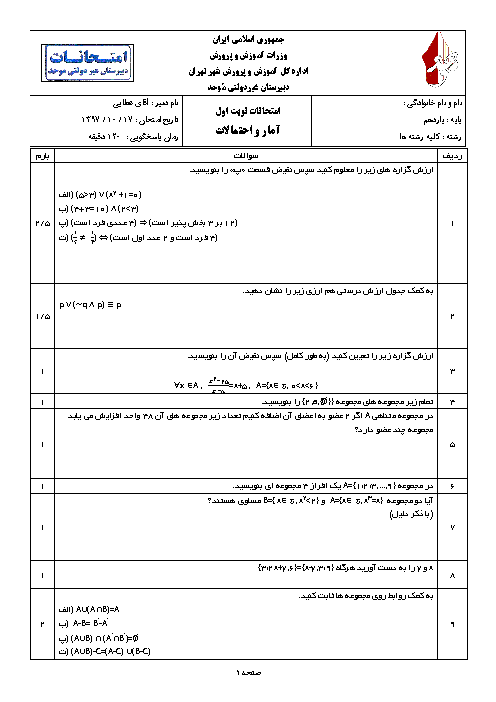
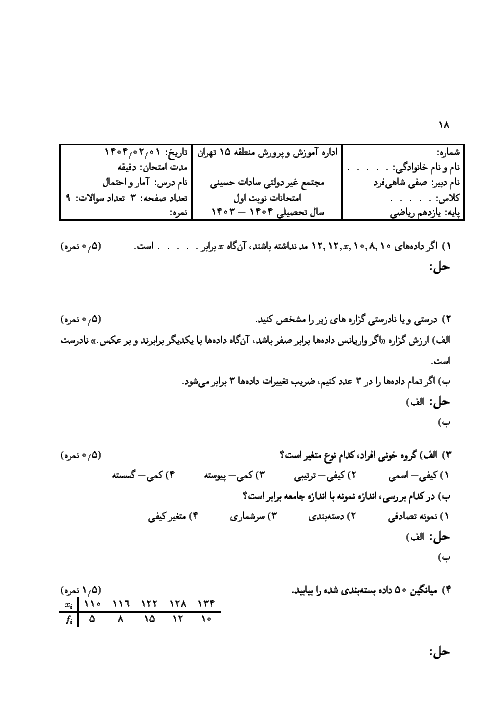
درس 4: پیشامدهای مستقل و وابسته آمار و احتمال یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

يك سكه و يك تاس را پرتاب می‌كنيم. احتمال آن‌كه سكه پشت و تاس زوج بيايد چقدر است؟

1 )

$\frac{1}{4}$

2 )

$\frac{1}{6}$

3 )

$\frac{1}{3}$

4 )

$\frac{1}{2}$

نمایش پاسخ

راه‌حل اول:

نکته: دو پیشامد A و B را مستقل می‌ناميم هرگاه وقوع هريك، بر وقوع ديگری تأثيری نداشته باشد. به عبارت ديگر، برای دو پيشامد مستقل A و B داریم: $P(A\cap B)=P(A)P(B)$

$A$ را پيشامد «پشت آمدن سکه» و $B$ را پیشامد «زوج آمدن عدد تاس» در نظر می‌گيريم. چون اين دو پيشامد مستقل‌اند، داريم:

$P(A\cap B)=P(A)P(B)=\frac{1}{2}\times \frac{3}{6}=\frac{1}{4}$

راه حل دوم: تعداد اعضای فضای نمونه‌ای برابر است با: $n(S)=2\times 6=12$

پیشامد «پشت آمدن سكه و زوج آمدن تاس» عبارت است از: {($6$ و پ)و ($4$ و پ) و ($2$ و پ)}= $A$

بنابراين احتمال موردنظر برابر است با: $P(A)=\frac{n(A)}{n(S)}=\frac{3}{12}=\frac{1}{4}$

گزارش اشکال