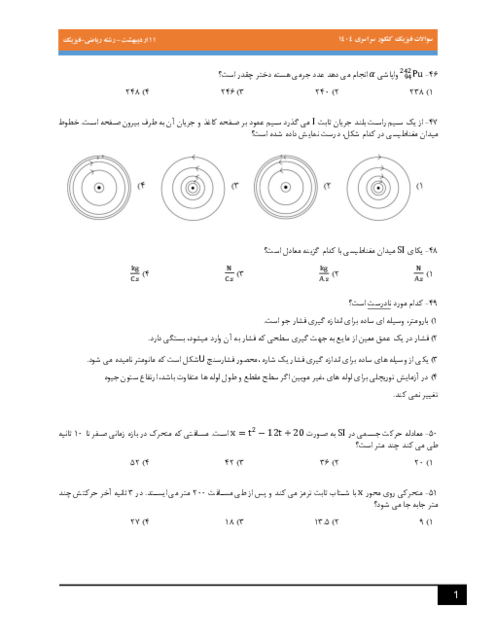
شکل مقابل، نمودار تغییرات انرژی جنبشی و پتانسیل سامانهٔ جرم - فنری را برحسب مکان نشان میدهد. اگر حداقل زمانی که طول میکشد که انرژی جنبشی نوسانگر از صفر به $40mJ$ برسد برابر $0/05s$ باشد، بزرگی سرعت نوسانگر در لحظهٔ عبور از مکان $x = 0$ چند متر بر ثانیه است؟