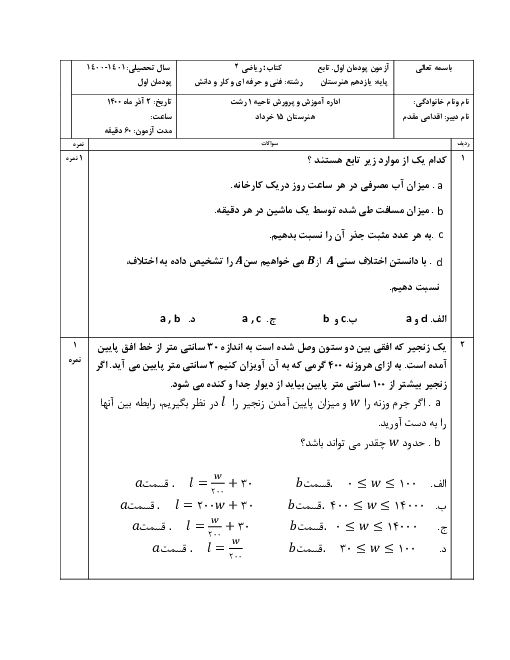
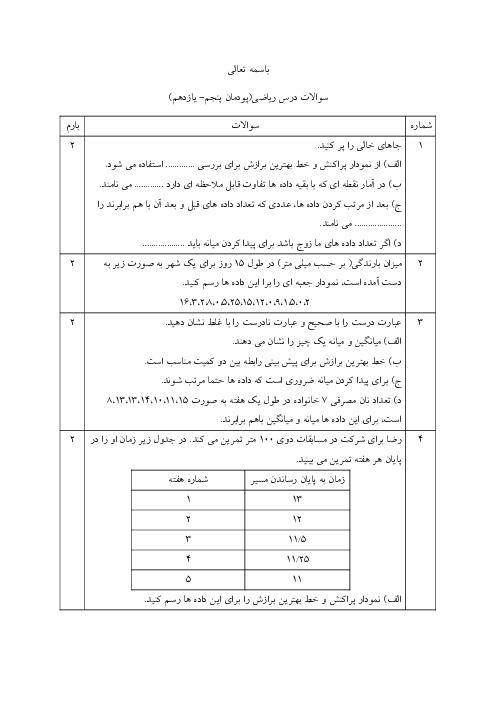
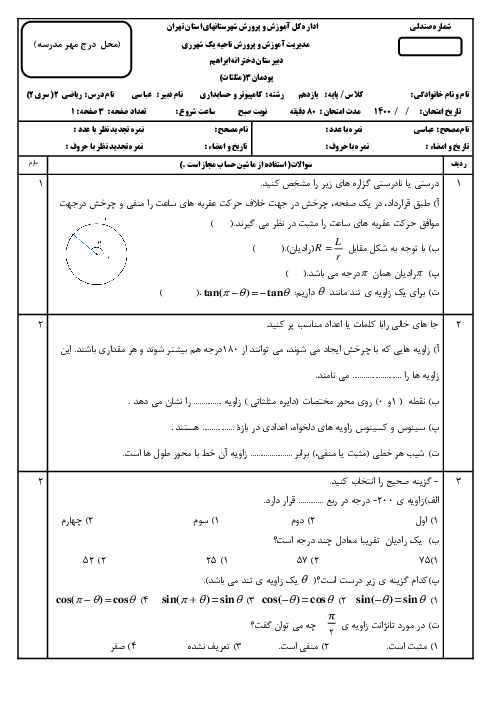
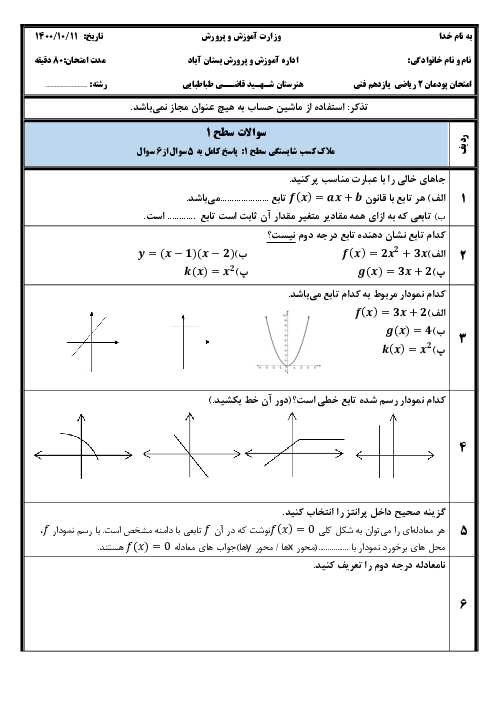
$x = \frac{\pi }{6} \to \frac{{4 - \frac{3}{2}\sin \left( {3 \times \frac{\pi }{6} - \pi } \right)}}{{ - 1 + \frac{1}{4}\cos \left( {2 \times \frac{\pi }{6} + \pi } \right)}}$

$ = \frac{{4 - \frac{3}{2}\sin \left( {\mathop {\cancel{{\frac{\pi }{2} - \pi }}}\limits^{\frac{{ - \pi }}{2}} } \right)}}{{ - 1 + \frac{1}{4}\cos \left( {\underline {\frac{\pi }{3} + \pi } } \right)}} = \frac{{4 - \frac{3}{2}( - 1)}}{{ - 1 + \frac{1}{4}\left( { - \frac{1}{2}} \right)}}$

در ربع سوم $cos$ منفی است پس $\cos \frac{\pi }{3}$

$ = \frac{{4 + \frac{3}{2}}}{{ - 1 - \frac{1}{8}}} = \frac{{\frac{{11}}{2}}}{{\frac{{ - 9}}{8}}} = \frac{{ - 44}}{9}$