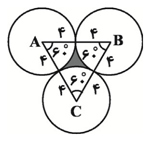
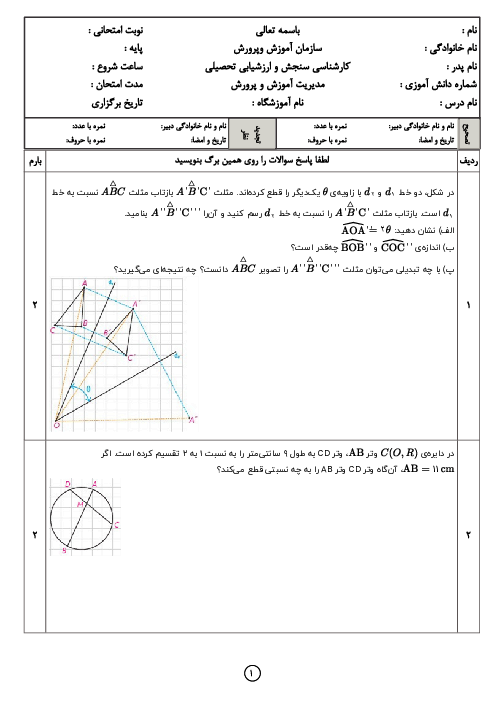
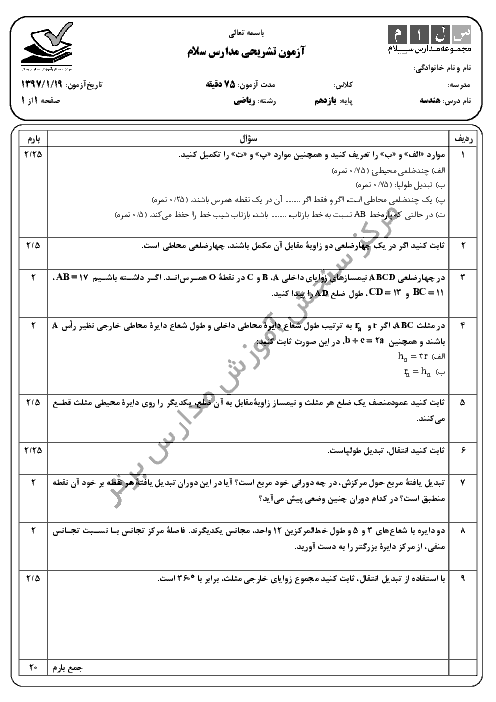
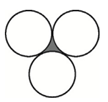
مطابق شكل سه دايره به شعاع‌های برابر 4، دوبه‌دو بر هم مماس‌اند. مساحت ناحيهٔ محدود به سه دايره كدام است؟
1 )
$4(\sqrt{3}-\frac{\pi }{4})$
2 )
$8(\sqrt{3}-\frac{\pi }{4})$
3 )
$8(\sqrt{3}-\frac{\pi }{2})$
$16(\sqrt{3}-\frac{\pi }{2})$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...