پودمان 4: لگاریتم و خواص آن
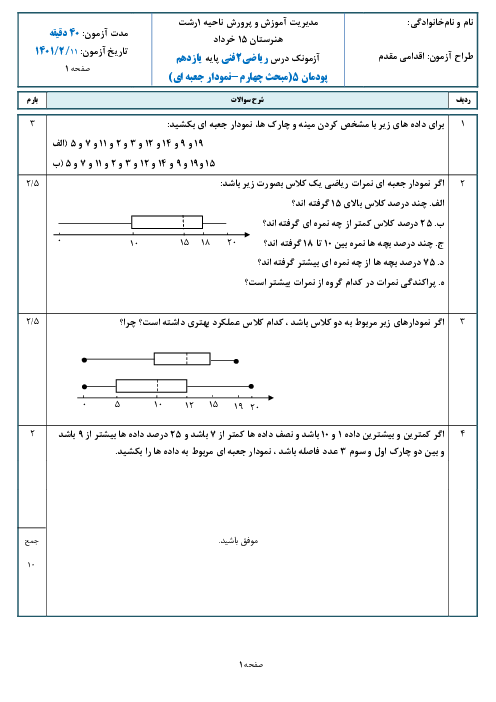
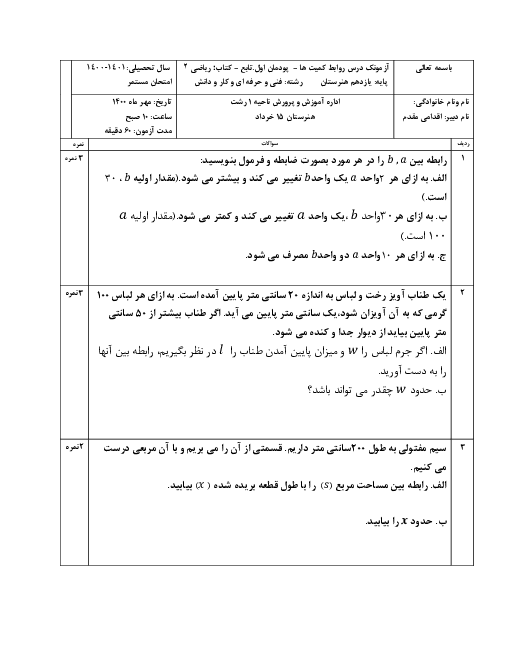
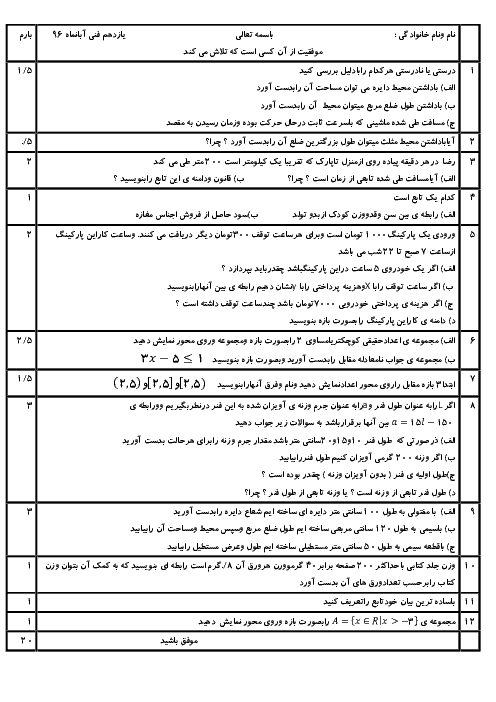
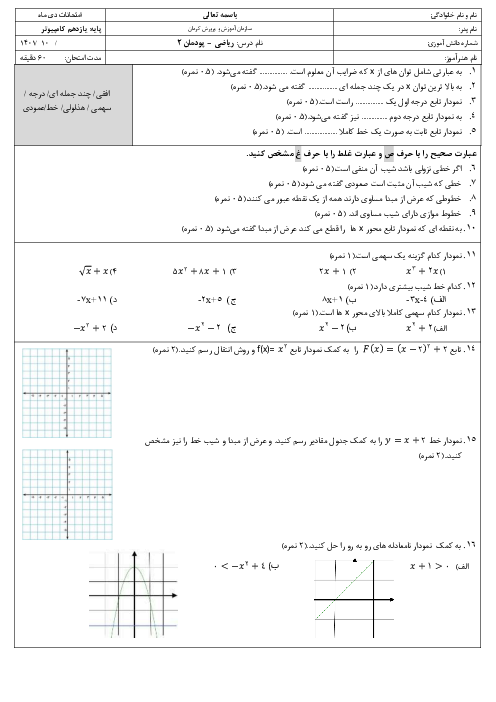
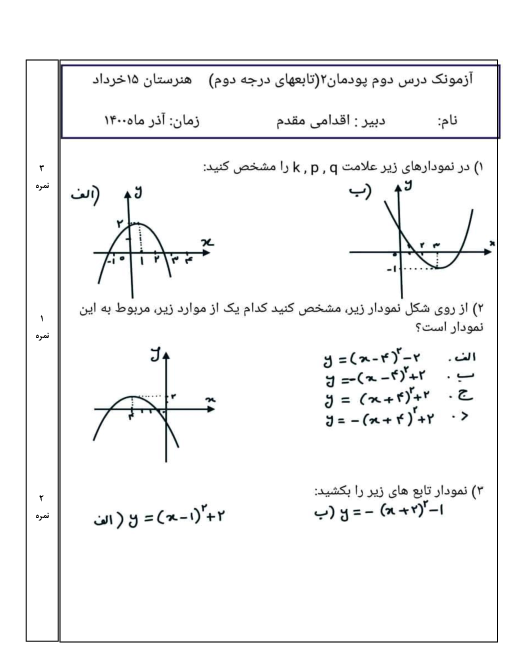
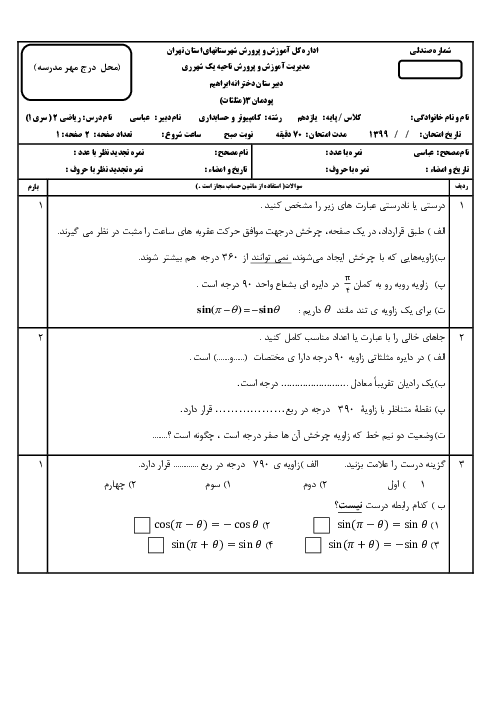
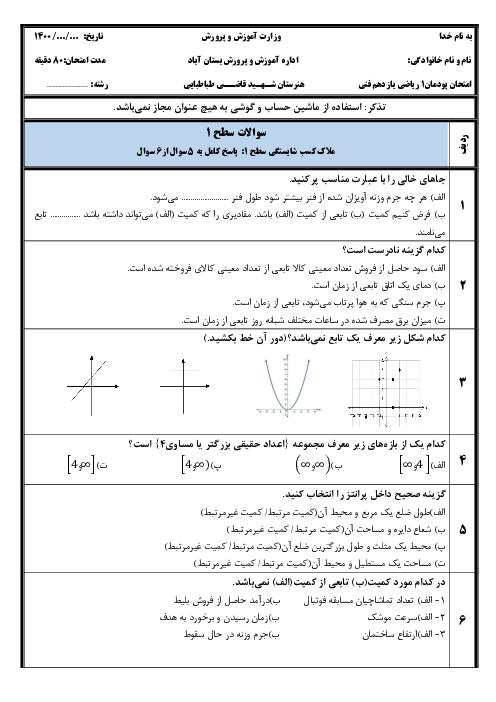
ریاضی2 فنی
یازدهم
دوره دوم متوسطه- فنی
مشترک شاخۀ فنی و حرفه‌ای
درسنامه آموزشی این مبحث
ساده شده‌ی عبارت $\frac{{{2^{(2\log _2^5 + 1)}}}}{{\log 0/0005}}$ کدام است؟ ($\log 2 \simeq 0/3$)
$ - \frac{{500}}{{33}}$
2 )
$ - \frac{{50}}{{33}}$
3 )
$\frac{{50}}{{33}}$
4 )
$\frac{{500}}{{33}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
آرزو لطیف 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...