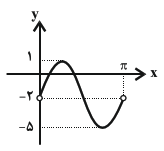
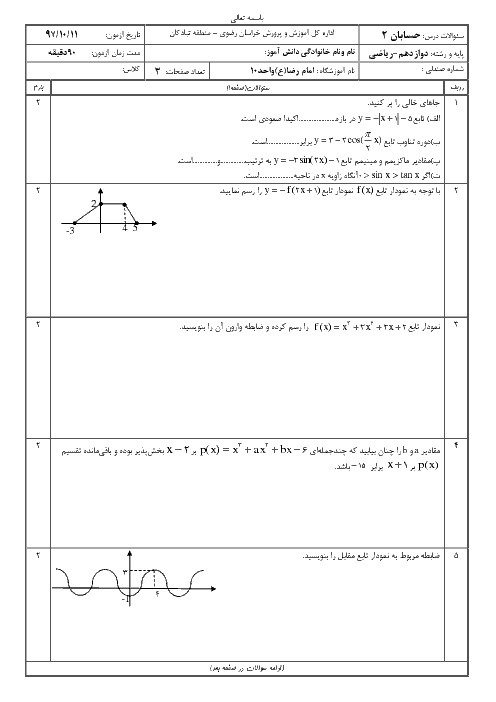
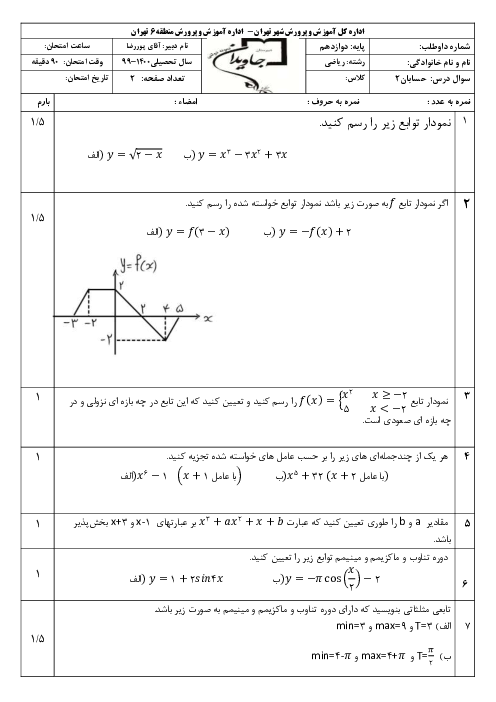
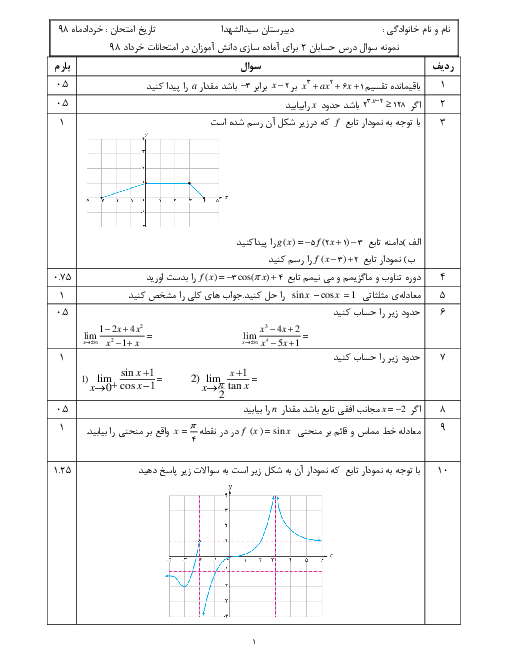
نمودار تابع‌های $f(x)=3\sin 2x-2$ و $g(x)=k$ در بازهٔ $(0,T)$ همدیگر را در دو نقطه قطع می‌کنند. حدود $k$ کدام است؟ ($T$ دورهٔ تناوب تابع $f$ است.)
1 )
$(-5,1)$
$(-5,-2)\bigcup (-2,1)$
3 )
$(-2,1)\bigcup (1,5)$
4 )
$(-7,-5)\bigcup (-5,-2)$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...