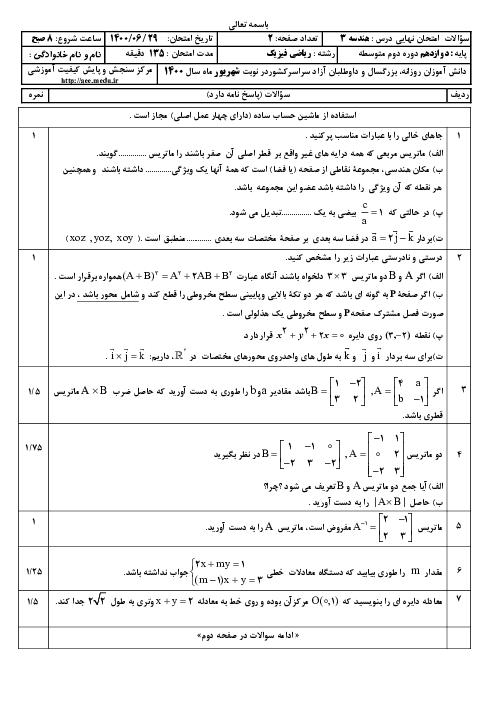
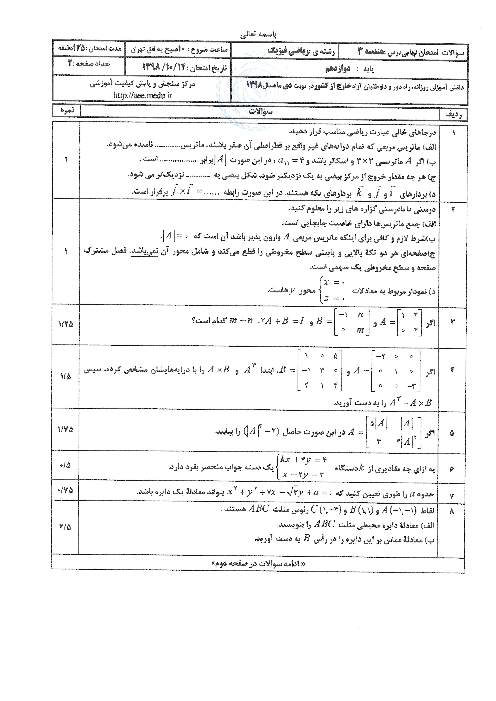
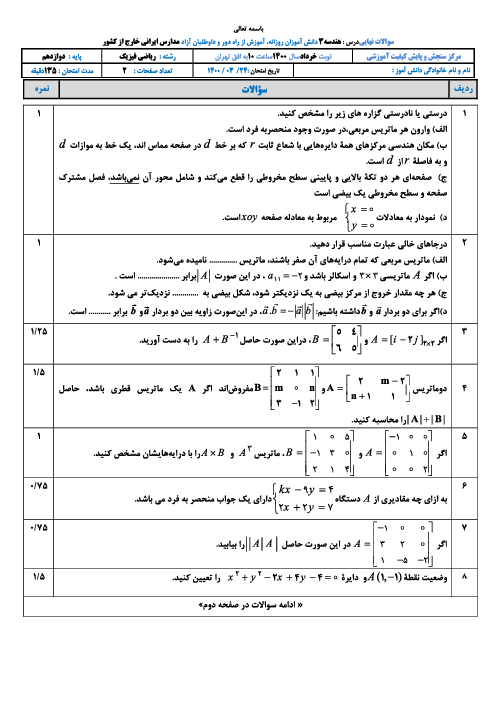
$CA=B+C\Rightarrow CA-C=B\Rightarrow C(A-I)=B$

$\Rightarrow C=B{{(A-I)}^{-1}}=\left[ \begin{matrix} \begin{matrix} 2  \\ 1  \\ \end{matrix} & \begin{matrix} 0  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right]{{\left( \left[ \begin{matrix} \begin{matrix} 0  \\ 0  \\ \end{matrix} & \begin{matrix} 1  \\ 2  \\ \end{matrix}  \\ \end{matrix} \right]-\left[ \begin{matrix} \begin{matrix} 1  \\ 0  \\ \end{matrix} & \begin{matrix} 0  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right] \right)}^{-1}}$$=\left[ \begin{matrix} \begin{matrix} 2  \\ 1  \\ \end{matrix} & \begin{matrix} 0  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right]{{\left( \left[ \begin{matrix} \begin{matrix} -1  \\ 0  \\ \end{matrix} & \begin{matrix} 1  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right] \right)}^{-1}}=\left[ \begin{matrix} \begin{matrix} 2  \\ 1  \\ \end{matrix} & \begin{matrix} 0  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right]\times (-1)\left[ \begin{matrix} \begin{matrix} 1  \\ 0  \\ \end{matrix} & \begin{matrix} -1  \\ -1  \\ \end{matrix}  \\ \end{matrix} \right]=$$\left[ \begin{matrix} \begin{matrix} 2  \\ 1  \\ \end{matrix} & \begin{matrix} 0  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right]\left[ \begin{matrix} \begin{matrix} -1  \\ 0  \\ \end{matrix} & \begin{matrix} 1  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} -2  \\ -1  \\ \end{matrix} & \begin{matrix} 2  \\ 2  \\ \end{matrix}  \\ \end{matrix} \right]\Rightarrow \left| C \right|=-4+2=-2$