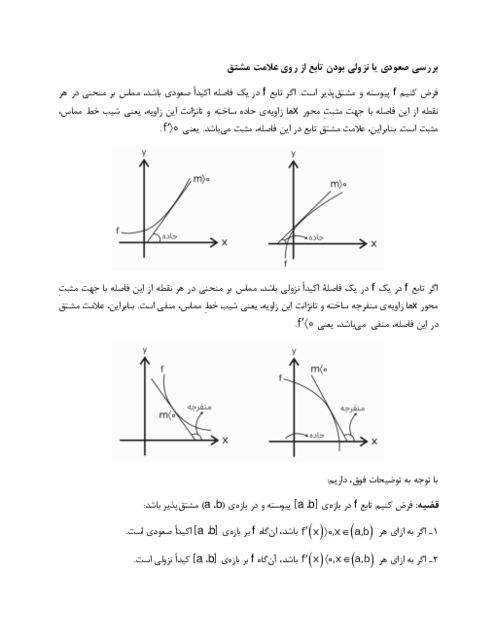
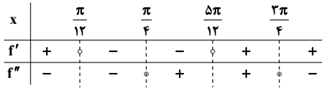
تابع $y=x-2{{\operatorname{Sin}}^{2}}x$ در كدام بازه نزولی و تقعر آن روبهپايين است؟
1 )
$(0,\frac{\pi }{12})$
$(\frac{\pi }{12},\frac{\pi }{4})$
3 )
$(\frac{\pi }{4},\frac{5\pi }{12})$
4 )
$(\frac{5\pi }{12},\frac{3\pi }{4})$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...