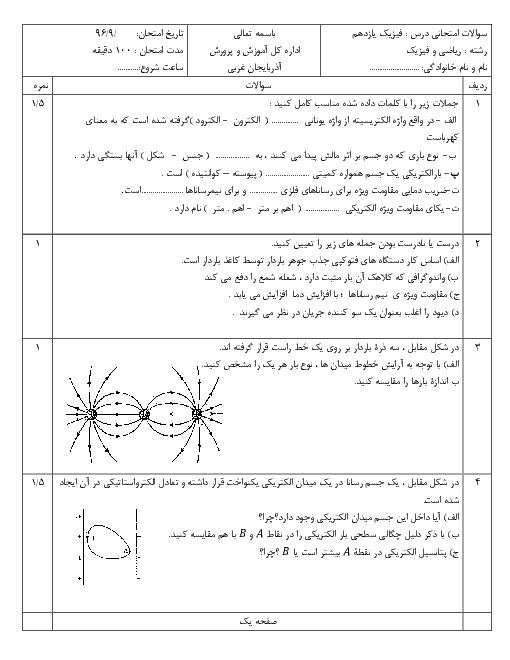
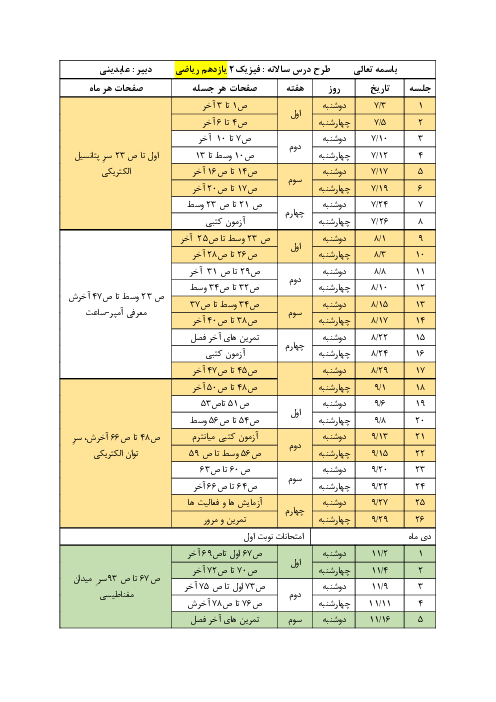
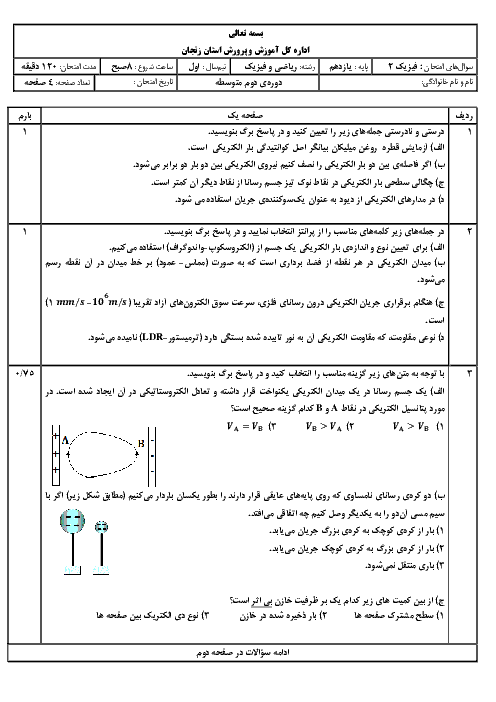
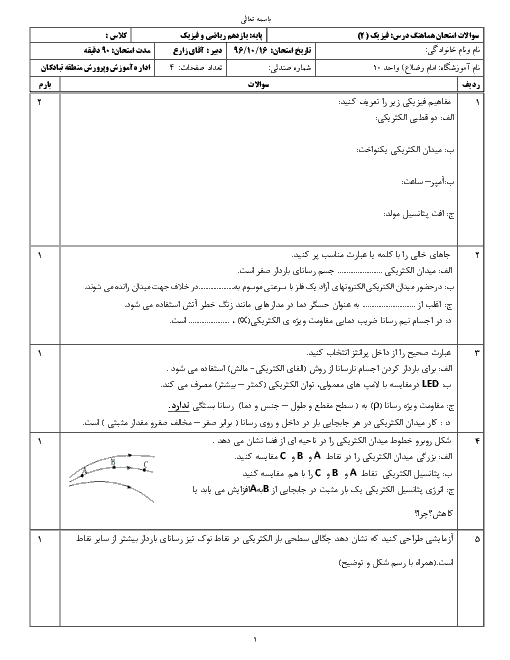
در حالت اول داریم:
${{\overrightarrow{E}}_{1}}+{{\overrightarrow{E}}_{2}}=\overrightarrow{E}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$
با کاهش 75٪ فاصلهٔ بار ${{q}_{1}}$ از مبدأ، فاصلهٔ آن از مبدا $\frac{1}{4}r$ میشود و میدان حاصل از بار ${{q}_{1}}$ در مبدا $(E\propto \frac{1}{{{r}^{2}}})$ 16 برابر میشود.
${{\overrightarrow{E}}^{\prime }}_{1}+{{\overrightarrow{E}}^{\prime }}_{2}=4\overrightarrow{E}\Rightarrow 16{{\overrightarrow{E}}_{1}}+{{\overrightarrow{E}}_{2}}=4\overrightarrow{E}\,\,\,\,\,\,\,\,\,\,\,\,(2)$
$\xrightarrow[{}]{(2),(1)}\left\{ \begin{matrix}
16{{\overrightarrow{E}}_{1}}+{{\overrightarrow{E}}_{2}}=4\overrightarrow{E} \\
{{\overrightarrow{E}}_{1}}+{{\overrightarrow{E}}_{2}}=\overrightarrow{E}\,\,\,\,\,\,\, \\
\end{matrix} \right.\Rightarrow \begin{matrix}
{{\overrightarrow{E}}_{1}}=0/2\overrightarrow{E} \\
{{\overrightarrow{E}}_{2}}=0/8\overrightarrow{E} \\
\end{matrix}$
چون میدانها در نقطهٔ O در یک جهت میباشند، پس بارها ناهمنام هستند. با مقایسهٔ میدان حاصل از دو بار در حالت اول داریم:
$E=k\frac{\left| q \right|}{{{r}^{2}}}\Rightarrow \frac{{{E}_{2}}}{{{E}_{1}}}=\left| \frac{{{q}_{2}}}{{{q}_{1}}} \right|\times {{(\frac{{{r}_{1}}}{{{r}_{2}}})}^{2}}\Rightarrow 4=(-\frac{{{q}_{2}}}{{{q}_{1}}})\times 1\Rightarrow \frac{{{q}_{2}}}{{{q}_{1}}}=-4$