در مثلث متساوی‌الاضلاع به ضلع ،شعاع دايرهٔ محاطی خارجی كدام است؟

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 3: چند ضلعی‌های محاطی و محیطی هندسه (2) یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

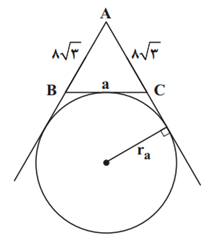
در مثلث متساوی‌الاضلاع به ضلع $8\sqrt{3}$،شعاع دايرهٔ محاطی خارجی كدام است؟

1 )

2 )

3 )

4 )

نمایش پاسخ

نکته: مساحت مثلث متساوی‌الاضلاع به ضلع a، برابر $\frac{\sqrt{3}}{4}{{a}^{2}}$ است.

نکته: در مثلث $ABC$ با مساحت $S$ و محیط $2P$، شعاع دایرهٔ محاطی خارجی نظیر رأس $A$ برابر است با: ${{r}_{a}}=\frac{S}{P-a}$

مساحت و محیط این مثلث عبارتند از:

مساحت: $S=\frac{\sqrt{3}}{4}{{a}^{2}}=\frac{\sqrt{3}}{4}\times 64\times 3=48\sqrt{3}$

محیط: $2P=8\sqrt{3}\times 3=24\sqrt{3}$

بنابراین شعاع دایرهٔ محاطی خارجی این مثلث برابر است با:

${{r}_{a}}=\frac{S}{P-a}=\frac{48\sqrt{3}}{12\sqrt{3}-8\sqrt{3}}=\frac{48\sqrt{3}}{4\sqrt{3}}=12$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1402/06/27

عباس ابراهیمی علویجه

محتوای متنی دوره آموزشی، هندسه (2) یازدهم دوره دوم متوسطه- نظری

مدرس: جابر عامری

مدت دوره: 162 صفحه (3 فایل)

با آلبوم تست، آزمون دلخواهتو بساز

سوپراستار

51 صفحه

کلید طلایی نمره 20 در امتحان هماهنگ کشوری هندسه 2 یازدهم رشته ریاضی فیزیک

کلاس یازدهمی

4 صفحه

آزمون نیمسال اول هندسه (2) یازدهم دبیرستان فاطمة الزهرا سیریک | دی 98

علی طاهری

7 صفحه

امتحان نوبت دوم هندسه 2 یازدهم دبیرستان دخترانه غیردولتی سما سنندج | خرداد…

محمدجواد باغبان باشی

4 صفحه

آزمون پایانی نوبت دوم هندسه (2) پایه یازدهم دبیرستان فرزانگان 2 تهران…

سلیمه خان احمدی

رایـــــگان

6 صفحه

آزمون آمادگی امتحان نوبت اول هندسه (2) پایه یازدهم ریاضی | دبیرستان سرای…

کلاس یازدهمی

2 صفحه

سوالات امتحان نوبت اول هندسه (2) پایه یازدهم دبیرستان غیرانتفاعی هاتف…

تیم مدیریت گاما

3 صفحه

امتحان ترم دوم هندسه (2) یازدهم دبیرستان ثقلین | خرداد 1401

علی بلقدر

48 صفحه

جزوه جامع فصل 3: روابط طولی در مثلث | هندسه سال یازدهم

حبیب هاشمی

2 صفحه

نمونه سؤال پیشنهادی امتحان نوبت دوم هندسه (2) پایۀ یازدهم رشته ریاضی +…

ریاضی دبیرستان

رایـــــگان

1 صفحه

آزمون نوبت دوم هندسه یازدهم تیزهوشان شهید صدوقی | خرداد 97

حسین نیکخواه

موارد بیشتر

ارسال فایل

چگونه مساحت مثلث با شعاع R را بدست آوریم؟

x و y را در اشکال زیر بیابید.

مساحت مثلث به طول اضلاع 3 و 4 و 5 به کمک دستور هرون حساب کنید.

موارد بیشتر

ارسال پرسش

موارد بیشتر

جستجوهای پرتکرار

پاسخ تشریحی :

تحلیل ویدئویی تست

با آلبوم تست

نمونه سوالات مشابه

اطلاع از تغییرات در بسته‌های گاما

کاربر عزیز سلام!

پاسخ تشریحی :

تحلیل ویدئویی تست

با آلبوم تست

نمونه سوالات مشابه