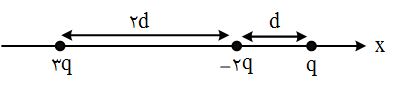
${F_{13}} = \frac{{K.(q)(3q)}}{{9{d^2}}} = \frac{{K{q^2}}}{{3{d^2}}} \leftarrow $
${F_{23}} = \frac{{K.(2q)(3q)}}{{4{d^2}}} = \frac{3}{2}\frac{{K{q^2}}}{{{d^2}}} \to $
${F_3} = {F_{23}} - {F_{13}} = \frac{{9k{q^2} - 2k{q^2}}}{{6{d^2}}} = \frac{{7k{q^2}}}{{6{d^2}}} \to $
${F_{12}} = \frac{{K.q.(2q)}}{{{d^2}}} = \frac{{2K{q^2}}}{{{d^2}}} \to $
${F_{32}} = {F_{23}} = \frac{3}{2}\frac{{K{q^2}}}{{{d^2}}} \leftarrow $
${F_2} = {F_{12}} - {F_{32}} = \frac{1}{2}\frac{{K{q^2}}}{{{d^2}}} \to $
$\frac{{{F_2}}}{{{F_3}}} = \frac{{\frac{1}{2}}}{{\frac{7}{6}}} = \frac{3}{7} \to {F_2} = \frac{3}{7}{F_3} = + \frac{3}{7}\vec F$