بررسی گزینهها
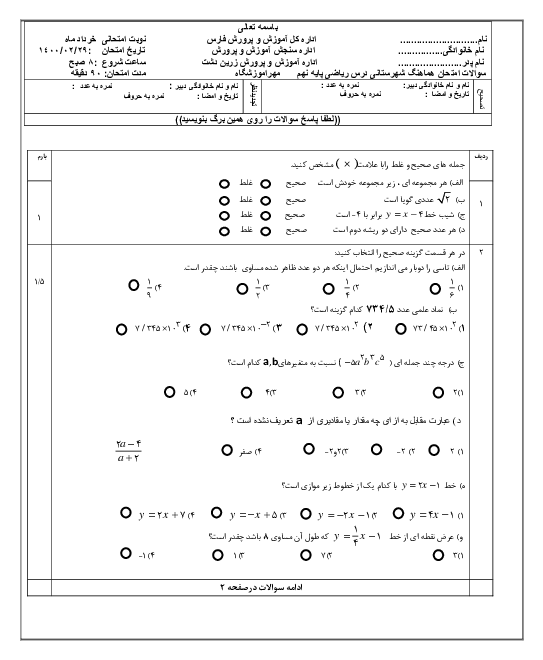
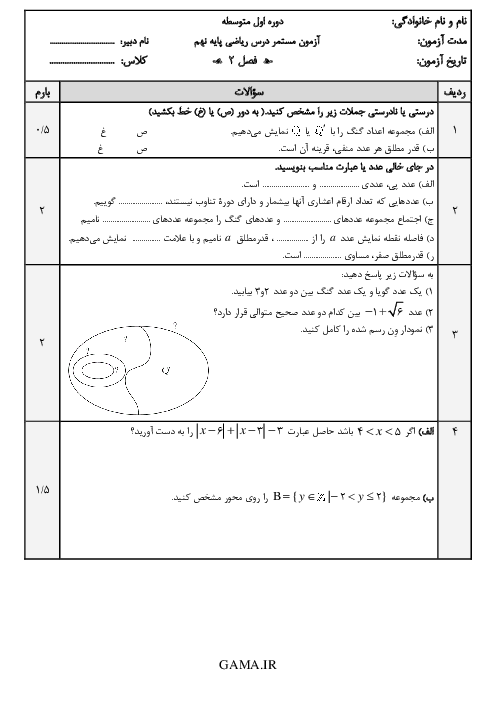
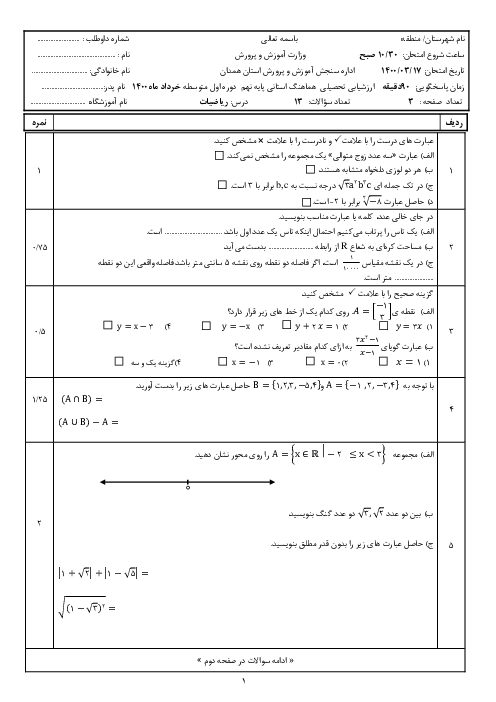
گزینه 1: توجه شود در صورت سوال، $ - 7 \leqslant n \leqslant - 5$ درست است.
$\left\{ { - 2n + 1|n \in \mathbb{Z}\,,\, - 7 \leqslant n \leqslant - 5} \right\} = \left\{ { - 2n + 1|n \in \left\{ { - 7, - 6, - 5} \right\}} \right\}$
$ = \left\{ { - 2( - 7) + 1\,,\, - 2( - 6) + 1\,,\, - 2( - 5) + 1} \right\} = \left\{ {11,13,15} \right\}$
گزینه 2:
$\begin{gathered}
\left\{ {n|n \in \mathbb{N}\,,\,11 \leqslant 2n + 1 \leqslant 15} \right\} = \left\{ {n|n \in \mathbb{N},\,10 \leqslant 2n \leqslant 14} \right\} \hfill \\
= \left\{ {n|n \in \mathbb{N}\,,\,5 \leqslant n \leqslant 7} \right\} = \left\{ {5,6,7} \right\} \hfill \\
\end{gathered} $
گزینه 3: ریشههای دوم مثبت مربعهای کامل فرد بین 100 و 256 عبارتند از:
$\left\{ {\sqrt {121} ,\sqrt {169} ,\sqrt {225} } \right\} = \left\{ {11,13,15} \right\}$
گزینه 4: برای به دست آوردن سه عدد فرد متوالی که حاصل جمع آنها 39 شود کافی است عدد کوچکتر را x و دو عدد دیگر بعد از آن را بهترتیب و در نظر بگیریم.
$x + \left( {x + 2} \right) + \left( {x + 4} \right) = 39 \Rightarrow 3x + 6 = 39 \Rightarrow 3x = 33 \Rightarrow x = 11$
بنابراین سه عدد فرد متوالی عضو مجموعهٔ $\left\{ {11,13,15} \right\}$ هستند.