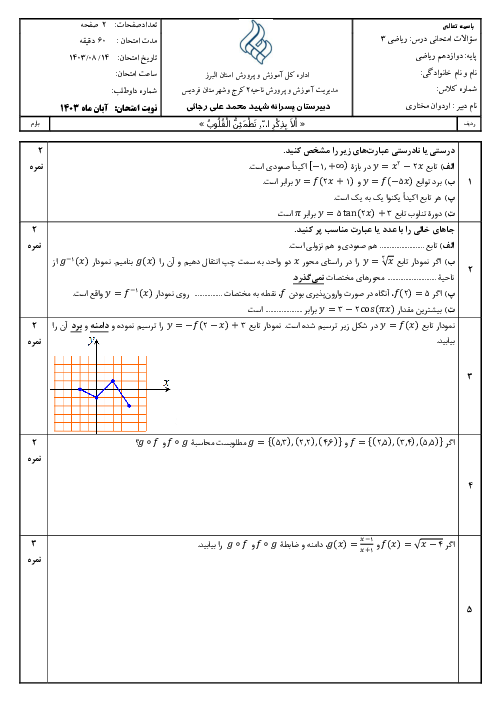
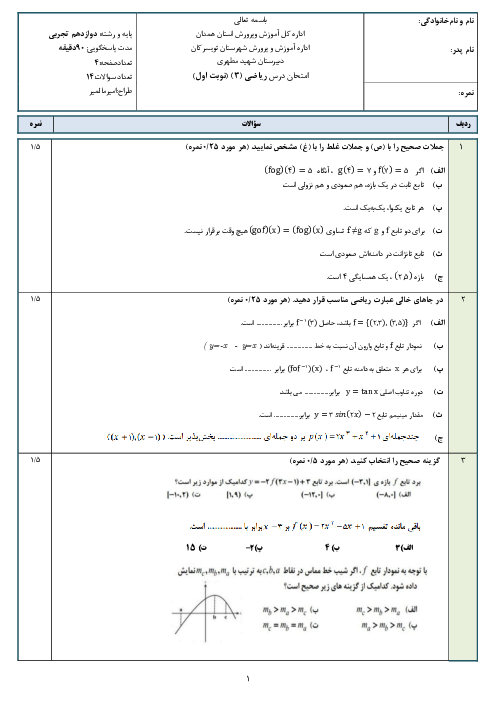
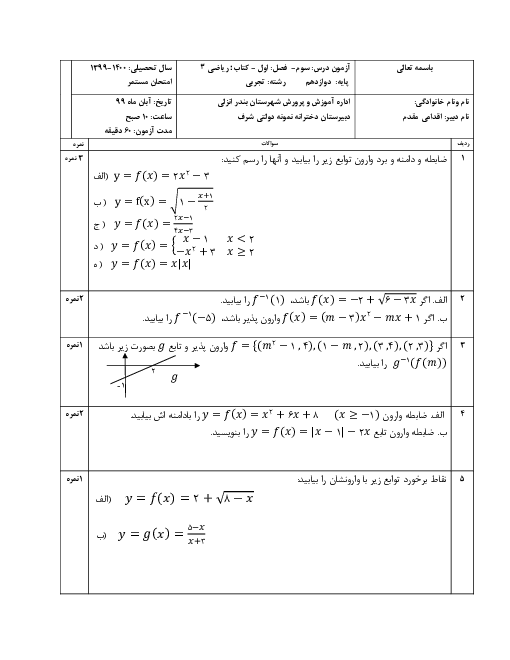
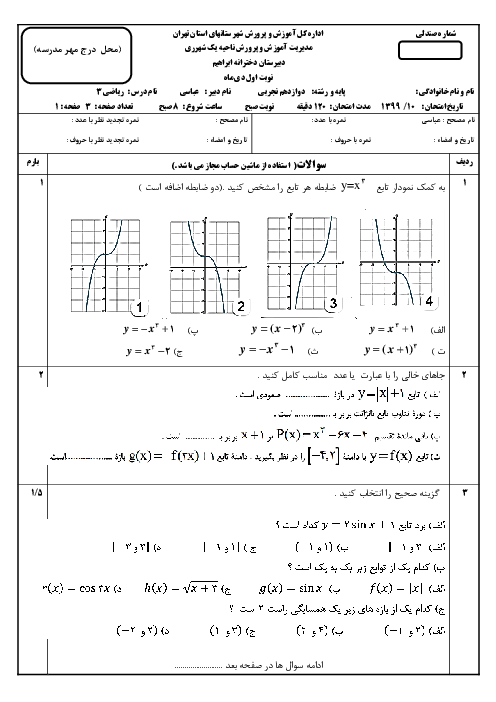
نکته: دامنه‌ی تابع $gof$ به‌صورت روبه‌رو تعریف می‌شود: ${{D}_{gof}}=\left\{ x\in {{D}_{f}}\left| f(x)\in {{D}_{g}} \right. \right\}$ 

ابتدا دامنه توابع $f$ و $g$ را به‌دست می‌آوریم:

$f(x)=\sqrt{x+2}\Rightarrow x+2\ge 0\Rightarrow x\ge -2\,\,\,\,,\,\,\,\,{{D}_{f}}=\left[ -2,+\infty  \right)$ 

$g(x)=\sqrt{{{x}^{2}}-16}\to {{x}^{2}}-16\ge 0\Rightarrow {{x}^{2}}\ge 16\Rightarrow x\le -4\,*\,x\ge 4\Rightarrow {{D}_{g}}=\left( -\infty ,-4 \right]\cup \left[ 4,+\infty  \right)$ 

${{D}_{gof}}=\left\{ x\in {{D}_{f}}\left| f(x)\in {{D}_{g}} \right. \right\}=\left\{ x\ge -2\left| f(x)\le -4\,*\,f(x)\ge 4 \right. \right\}$ 

$f(x)\le -4\,*\,f(x)\ge 4\Rightarrow \underbrace{\sqrt{x+2}\le -4}_{Gheyere\,Momken}\,*\,\sqrt{x+2}\ge 4\Rightarrow \sqrt{x+2}\ge 4\Rightarrow x+2\ge 16\Rightarrow x\ge 14$ 

${{D}_{gof}}=\left\{ x\ge -2\left| x\ge 14 \right. \right\}=\left[ 14,+\infty  \right)$