فصل 3: حد بینهایت و حد در بینهایت
ریاضی (3)
دوازدهم
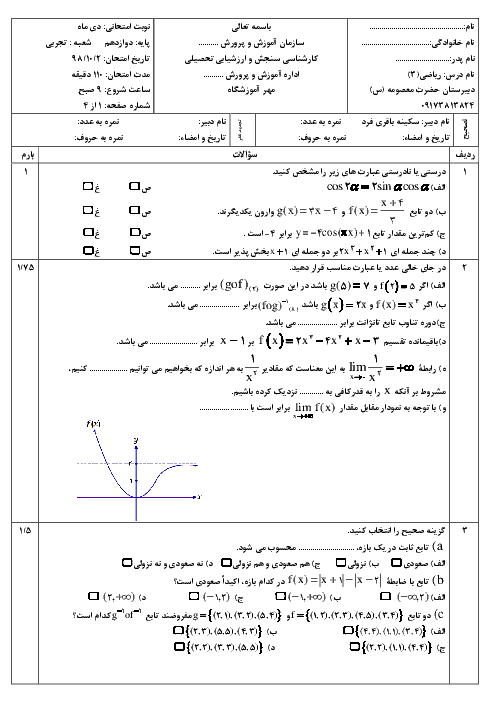
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
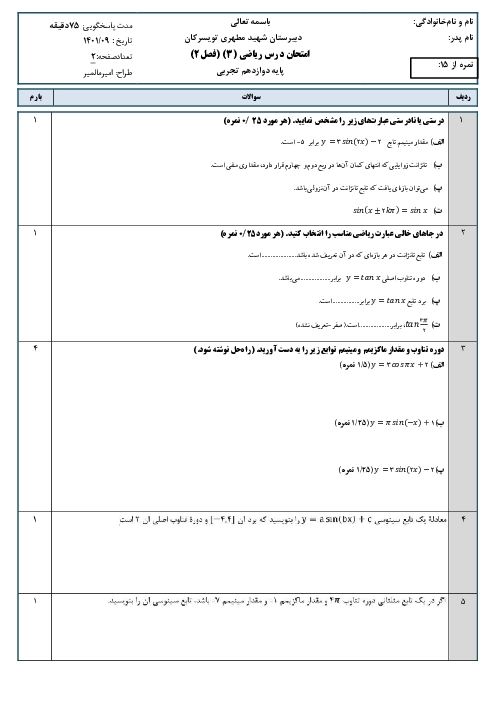
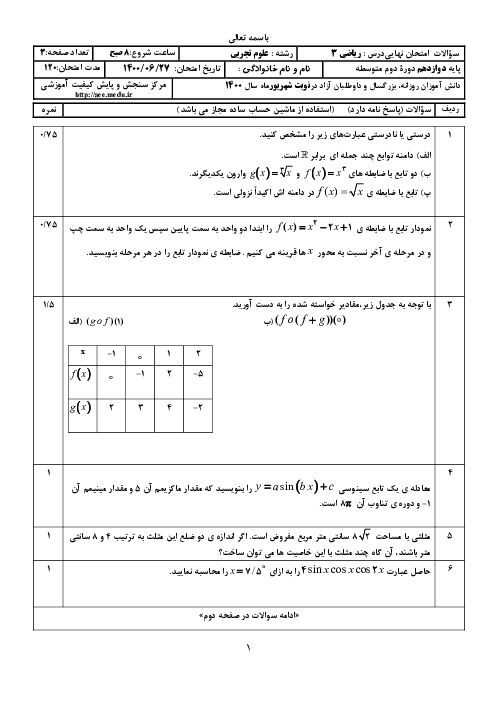
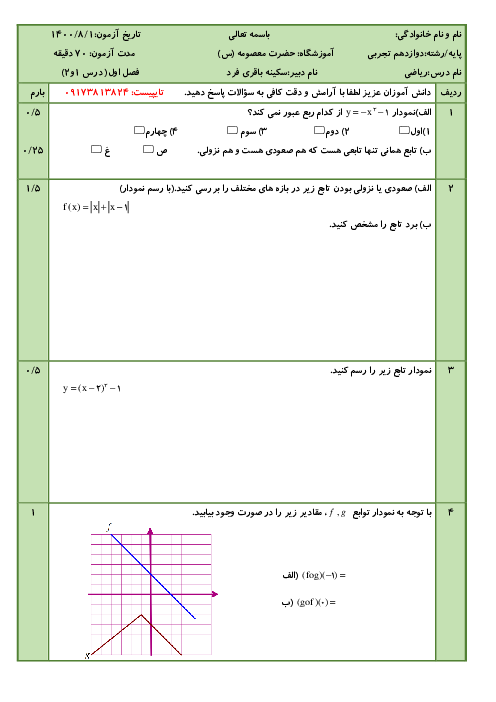
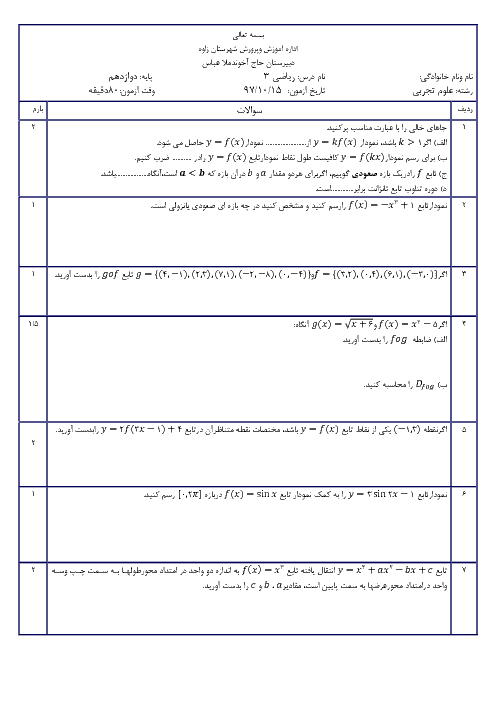
اگر $f(x)=\frac{\left| {{x}^{2}}-4 \right|}{x+1}$، حاصل $\underset{x\to +\infty }{\mathop{\lim }}\,xf(2+\frac{1}{x})$ کدام است؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!