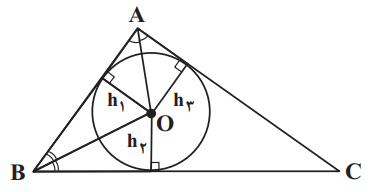
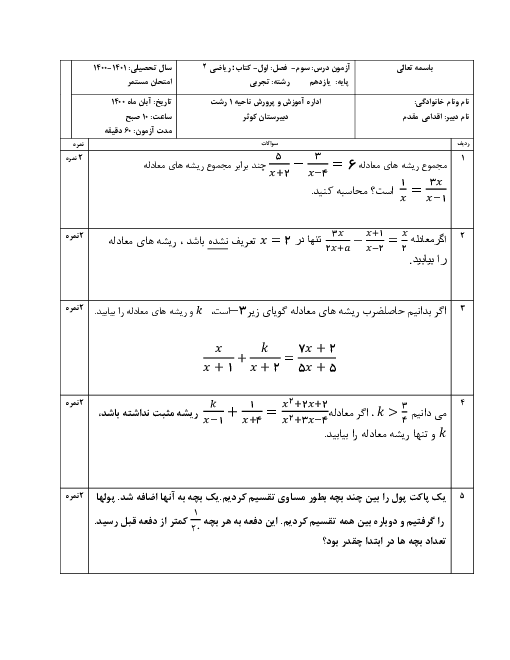
نقاط $B$، $A$ و $C$ رأس‌های مثلث دلخواه $ABC$ هستند. محل تلاقی نیمسازهای زاویه‌ای $A$ و $B$ را $O$ می‌نامیم. فاصلهٔ این نقطه را از اضلاع مثلث، ${{h}_{2}}$،${{h}_{1}}$ و ${{h}_{3}}$ می‌نامیم. کدام گزینه در مورد این فاصله‌ها درست است؟
1 )
${{h}_{1}}+{{h}_{2}}+{{h}_{3}}=1$
2 )
$\frac{{{h}_{1}}+{{h}_{2}}}{{{h}_{3}}}=3$
3 )
${{h}_{1}}{{h}_{2}}{{h}_{3}}=1$
${{h}_{1}}={{h}_{2}}={{h}_{3}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...