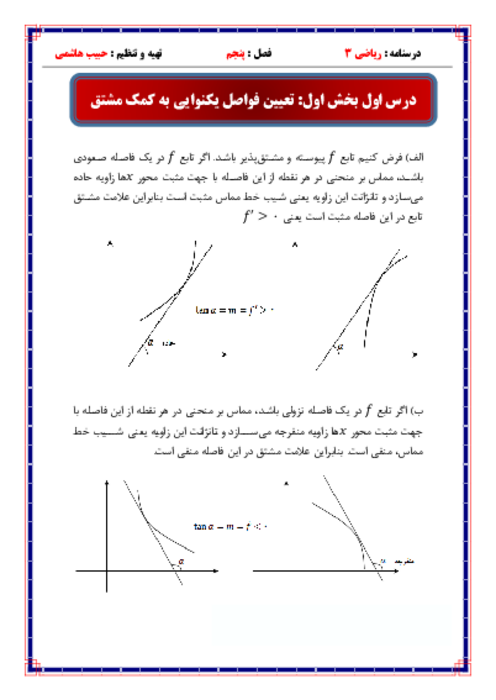
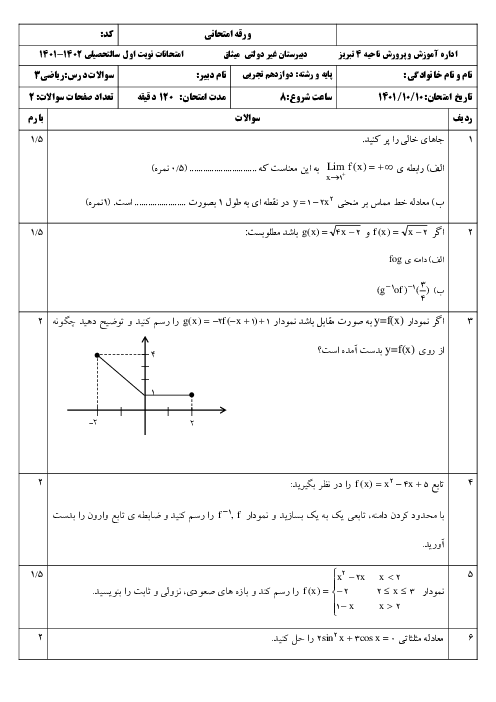
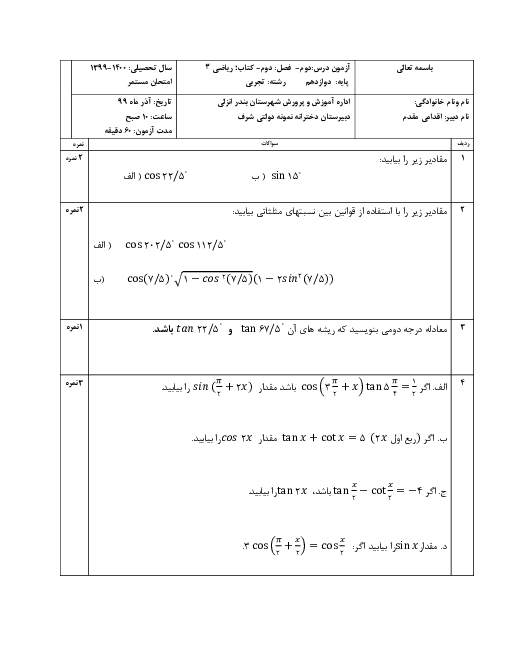
** فصل 3: حد بی‌نهایت و حد در بی‌نهایت
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
حد توابع زیر را در صورت وجود بیابید.
الف) $\mathop {\lim }\limits_{x \to 4} \frac{{2 - \sqrt x }}{{{x^2} - 16}}$
ب) $\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{1 - \cos x}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
هاشم مروانی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...