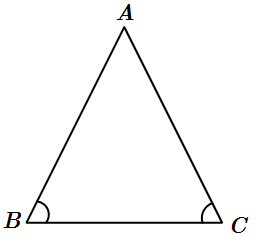
«در مثلث زیر دو زاویه‌ی B و C با هم مساوی‌اند. ثابت کنید مثلث ABC متساوی الساقین است». چند مورد از استدلال‌های زیر برای اثبات مسئله فوق معتبر است؟
الف) با استفاده از خط کش و اندازه گیری دو ضلع AB و AC نشان می‌دهیم که AB=AC است و در نتیجه مثلث متساوی الساقین است.
ب) ارتفاع وارد بر ضلع BC را رسم می کنیم دو مثلث ایجاد شده به حالت (و ز) هم‌نهشتند، پس بنا به اجزای متناظر AB=AC است و در نتیجه مثلث متساوی‌الساقین است.
ج) نیمساز زاویه‌ی A را رسم کرده دو مثلث ایجاد شده به حالت (ز ض ز) هم‌نهشتند پس بنا به اجزای متناظر AB=AC و در نتیجه مثلث متساوی‌الساقین است.
د) میانه وارد بر BC را رسم می‌کنیم دو مثلث ایجاد شده به حالت (ض ض ض) هم‌نهشتند پس بنا به اجزای متناظر AB=AC و در نتیجه مثلث متساوی‌الساقین است.
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...