درس 2: ضرب داخلی و ضرب خارجی بردارها
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
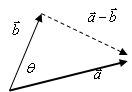
دو بردار ${\vec a}$ و ${\vec b}$ دارای طول‌های مساوی و زاویهٔ بین این دو بردار $\theta $ است. با توجه به شکل، ثابت کنید:
$\left| {\vec a - \vec b} \right| = 2\left| {\vec a} \right|\sin \frac{\theta }{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...