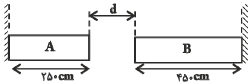
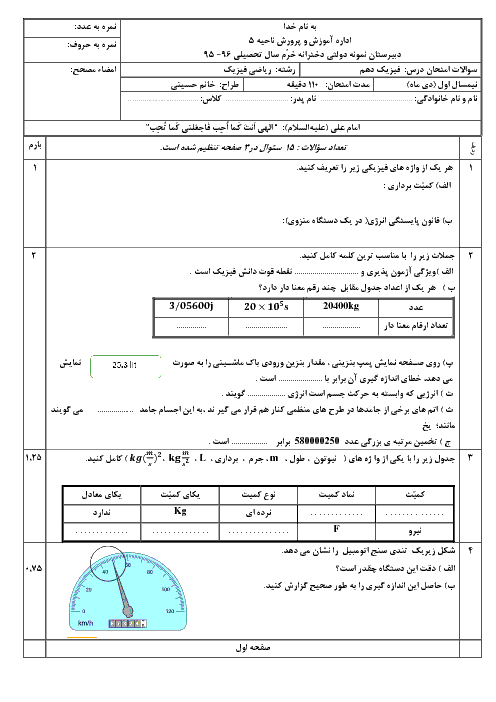
هر چه دما نسبت به سردترين دمای ممكن بيش‌تر باشد، تغيير طول ميله‌ها نيز بيش‌تر است. حداقل فاصله‌ی d هنگامی است كه در بالاترين دما، مجموع افزايش طول ميله‌ها برابر با d شود.

$\left\{ _{{{L}_{1(B)}}=450cm=45\times {{10}^{2}}mm\Rightarrow {{\alpha }_{B}}=3\times {{10}^{-5}}\frac{1}{K},\Delta {{T}_{B}}={{50}^{\circ }}c\Rightarrow \Delta {{L}_{B}}={{L}_{1(B)}}{{\alpha }_{B}}\Delta {{T}_{B}}=45\times {{10}^{+2}}\times 3\times {{10}^{-5}}\times 5\times {{10}^{1}}\Rightarrow \Delta {{L}_{B}}=6/75mm}^{{{L}_{1(A)}}=250cm=25\times {{10}^{2}}mm\Rightarrow {{\alpha }_{A}}=2\times {{10}^{-5}}\frac{1}{K},\Delta {{T}_{A}}={{50}^{\circ }}c\Rightarrow \Delta {{L}_{A}}={{L}_{1(A)}}{{\alpha }_{A}}\Delta {{T}_{A}}=25\times {{10}^{+2}}\times 2\times {{10}^{-5}}\times 5\times {{10}^{1}}\Rightarrow \Delta {{L}_{A}}=2/5mm}\Rightarrow d=\Delta {{L}_{A}}+\Delta {{L}_{B}}=2/5+6/75=9/25mm \right.$