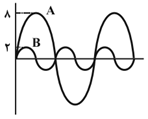
برای به‌دست آوردن ${{\beta }_{A}}-{{\beta }_{B}}$ باید نسبت $\frac{{{I}_{A}}}{{{I}_{B}}}$ را داشته باشیم. بنابراین ابتدا از رابطهٔ $\frac{{{I}_{A}}}{{{I}_{B}}}={{\left( \frac{{{A}_{A}}}{{{A}_{B}}}\times \frac{{{f}_{A}}}{{{f}_{B}}}\times \frac{{{r}_{B}}}{{{r}_{A}}} \right)}^{2}}$، نسبت $\frac{{{I}_{A}}}{{{I}_{B}}}$ را می‌یابیم. با توجه به شکل (واحد) ${{A}_{A}}=8$ و (واحد) ${{A}_{B}}=2$ و ${{\lambda }_{B}}=\frac{{{\lambda }_{A}}}{2}$ است. با توجه به اين‌كه در اين محيط تندی انتشار موج برای هر دو موج يكسان است، می‌توان نوشت:

${{\lambda }_{B}}=\frac{{{\lambda }_{A}}}{2}\Rightarrow \frac{{{\lambda }_{B}}}{{{\lambda }_{A}}}=\frac{1}{2}$

$f=\frac{v}{\lambda }\xrightarrow{v}\frac{{{f}_{A}}}{{{f}_{B}}}=\frac{{{\lambda }_{B}}}{{{\lambda }_{A}}}\Rightarrow \frac{{{f}_{A}}}{{{f}_{B}}}=\frac{1}{2}$

$\frac{{{I}_{A}}}{{{I}_{B}}}={{\left( \frac{{{A}_{A}}}{{{A}_{B}}}\times \frac{{{f}_{A}}}{{{f}_{B}}}\times \frac{{{r}_{B}}}{{{r}_{A}}} \right)}^{2}}\xrightarrow[{{A}_{A}}=8]{{{r}_{A}}={{r}_{B}},{{A}_{B}}=2}\frac{{{I}_{A}}}{{{I}_{B}}}={{\left( \frac{8}{2}\times \frac{1}{2}\times 1 \right)}^{2}}={{2}^{2}}$

اکنون می‌توان نوشت:

${{\beta }_{A}}-{{\beta }_{B}}=10\log \frac{{{I}_{A}}}{{{I}_{B}}}\Rightarrow {{\beta }_{A}}-{{\beta }_{B}}=10\log {{2}^{2}}=20\log 2\xrightarrow{\log 2=0/3}{{\beta }_{A}}-{{\beta }_{B}}=20\times 0/3=6dB$