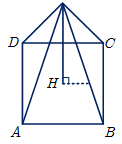
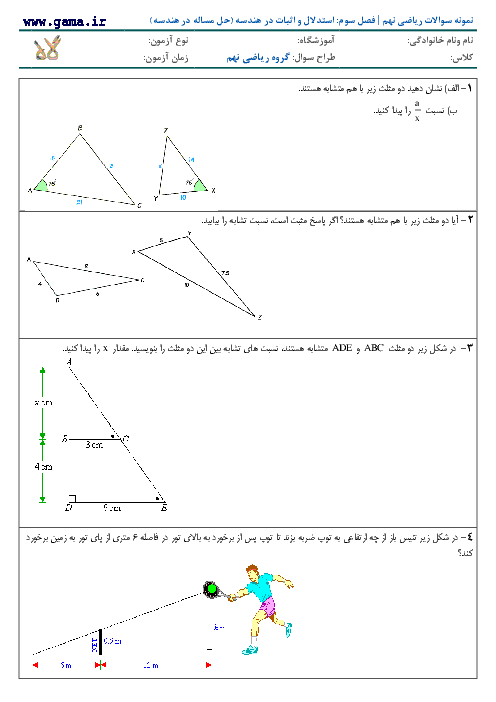
رابطهٔ فیثاغورس در مثلث ABD برقرار است:
$A{D^2} + A{B^2} = D{B^2}$
$ \Rightarrow D{B^2} = 16 + 16 = 32 \Rightarrow DB = \sqrt {32} = 4\sqrt 2 $
$ \Rightarrow HB = 2\sqrt 2 $
بنابراین با استفاده از رابطهٔ فیثاغورس داریم:
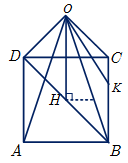
$\mathop {OHB}\limits^\Delta :O{H^2} + H{B^2} = O{B^2} \Rightarrow O{H^2} = O{B^2} - H{B^2}$
$ = 16 - 8 = 8 \Rightarrow OH = 2\sqrt 2 $
$BK = \frac{4}{2} = 2 \Rightarrow \mathop {OBK}\limits^\Delta :O{K^2} = O{B^2} - B{K^2}$
$ \Rightarrow O{K^2} = 16 - 4 = 12 \Rightarrow OK = 2\sqrt 3 $
مساحت جانبی $ = \frac{{4 \times \left( {4 \times 2\sqrt 3 } \right)}}{2} = 16\sqrt 3 $
مساحت کل $ = 16\sqrt 3 + 16 = 16(\sqrt 3 + 1)$
حجم $ = \frac{1}{3}S \times h = \frac{1}{3} \times 4 \times 4 \times 2\sqrt 2 = \frac{{32\sqrt 2 }}{3}$