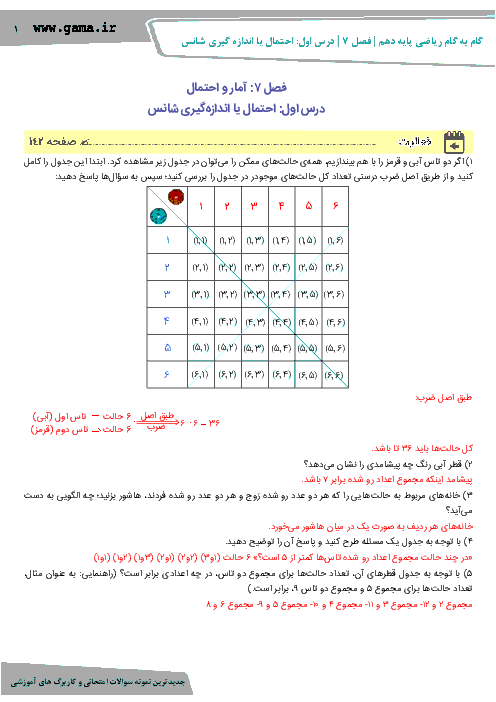
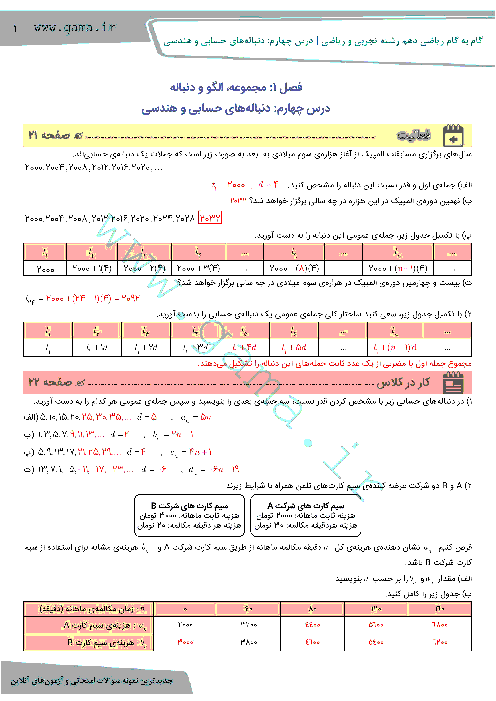
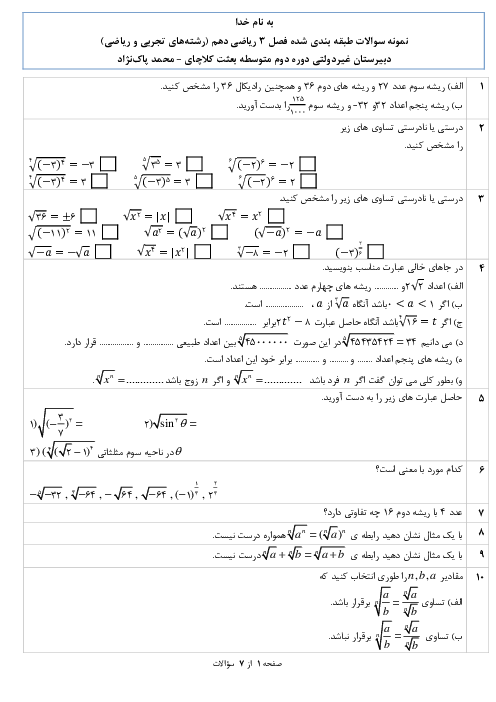
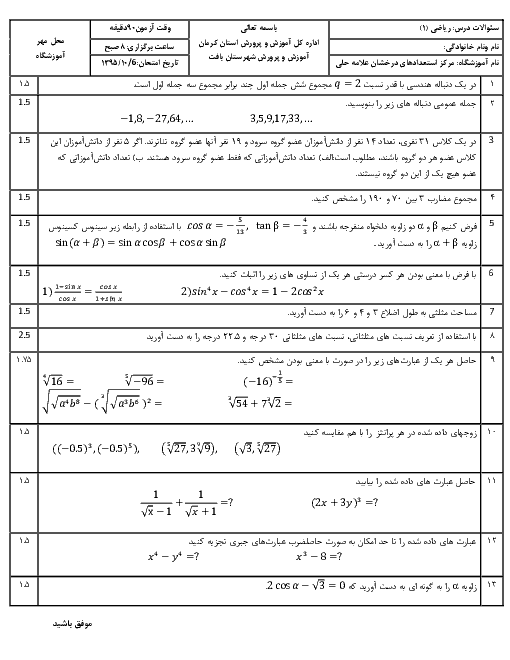
درس 1: معادلۀ درجه دوم و روشهای مختلف حل آن
ریاضی (1)
دهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
حدود $m$ کدام باشد تا $x=-1$ بین دو ریشهی معادلهی $x^{2}+mx+2m-3=0$ قرار بگیرد؟
1 )
$(6, + \infty)$
2 )
$(-2, + \infty)$
3 )
$(-\infty , 6)$
$(-\infty , 2)$