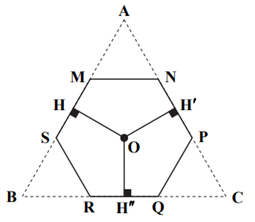
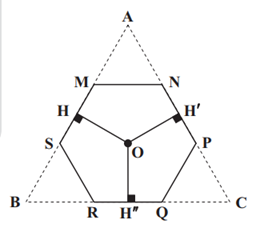
نکتهٔ 1: مجموع فواصل هر نقطهٔ دلخواه داخل مثلث متساوی‌الاضلاع از سه ضلع، برابر با اندازهٔ ارتفاع مثلث است.

نکتهٔ 2: اندازهٔ ارتفاع مثلث متساوی‌الاضلاع به طول ضلع a برابر است با: $\frac{\sqrt{3}}{2}a$

نکتهٔ 3: مساحت هر شش‌ضلعی منتظم به طول ضلع a، برابر است با: $\frac{3\sqrt{3}}{2}{{a}^{2}}$

نکتهٔ 4: مجموع زاویه‌های داخلی یک nضلعی برابر است با: $(n-2)\times 180{}^\circ $

با توجه به نکتهٔ 4 اندازهٔ هر زاویهٔ داخلی شش‌ضلعی منتظم برابر است با: $\frac{(6-2)\times {{180}^{{}^\circ }}}{6}={{120}^{{}^\circ }}$

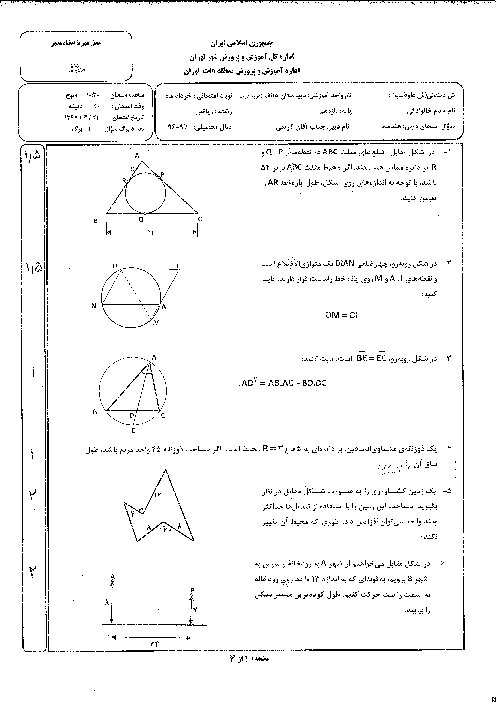
بنابراین در مثلث $AMN$ اندازهٔ دو زاویهٔ خارجی $(\hat{N},\hat{M})$ برابر ${{120}^{{}^\circ }}$ است، پس اندازهٔ زاویه‌های داخلی نظیر آن‌ها برابر ${{60}^{{}^\circ }}$ است. با توجه به اینکه مجموع زاویه‌های داخلی هر مثلث ${{180}^{{}^\circ }}$ است، نتیجه می‌گیریم اندازهٔ زاویهٔ $A$ هم برابر ${{60}^{{}^\circ }}$ است، پس مثلث $AMN$ متساوی‌الاضلاع است. بنابراین: $AM=AN=MN$

به همین ترتیب ثابت می‌شود. $BS=BR=SR,PC=QC=PQ$

بنابراین مثلث $ABC$ متساوی‌الاضلاع است و طول ضلع آن 3 برابر طول ضلع شش‌ضلعی منتظم است. اگر طول ضلع مثلث $ABC$ را a در نظر بگیریم، با توجه به نکته‌های 1 و 2 داریم: $OH+O{H}'+O{H}''=\sqrt{3}\Rightarrow \frac{\sqrt{3}}{2}a=\sqrt{3}\Rightarrow a=2$

بنابراین طول ضلع شش‌ضلعی که $\frac{1}{3}$ طول ضلع مثلث $ABC$ است، برابر می‌شود با: $\frac{a}{3}=\frac{2}{3}$

حال با توجه به نکتهٔ 3، مساحت شش‌ضلعی برابر است با: $S=\frac{3\sqrt{3}}{2}\times {{(\frac{2}{3})}^{2}}=\frac{3\sqrt{3}}{2}\times \frac{4}{9}=\frac{2\sqrt{3}}{3}$