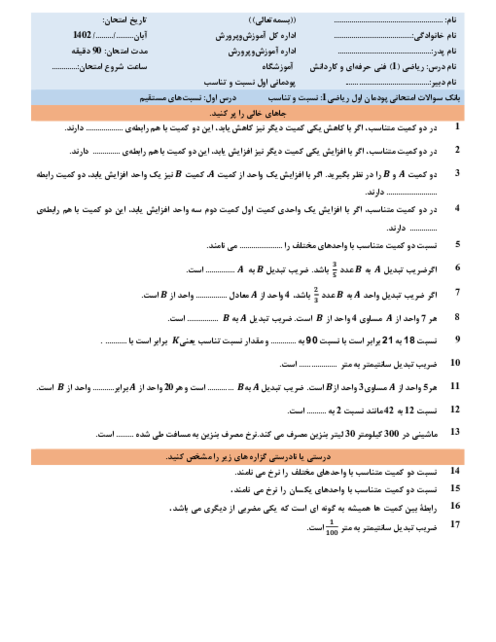
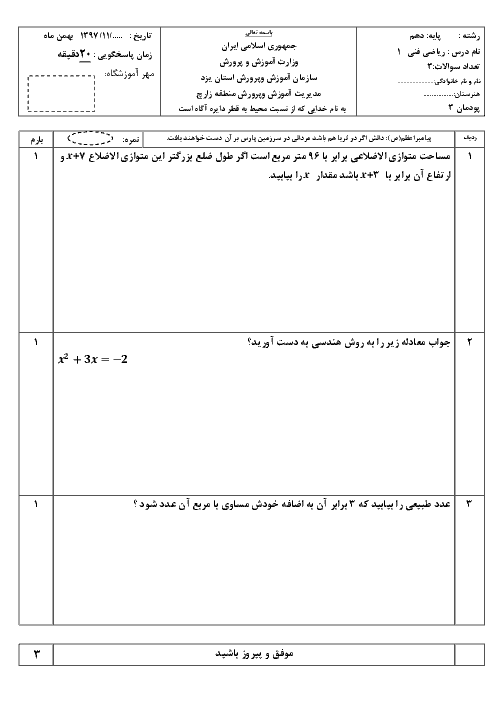
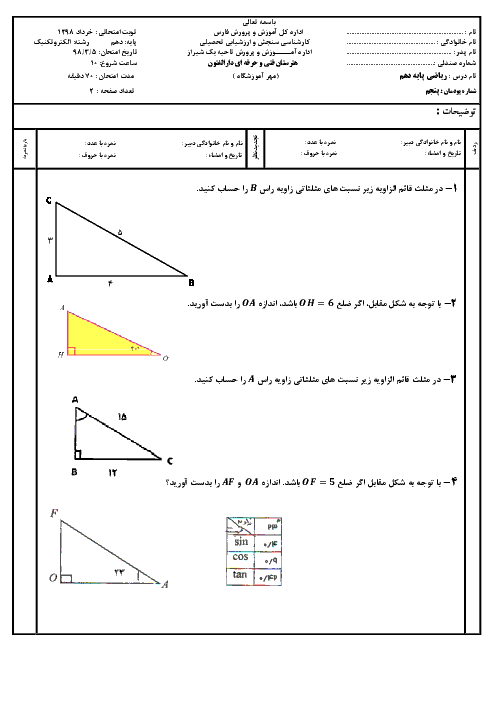
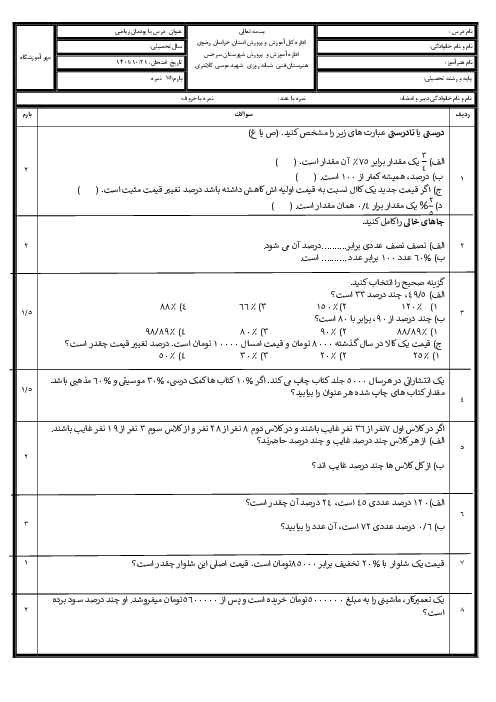
پودمان 3: معادله‌های درجۀ دوم
ریاضی1 فنی
دهم
دوره دوم متوسطه- فنی
مشترک شاخۀ فنی و حرفه‌ای
درسنامه آموزشی این مبحث
به ازای کدام مقدار $a$، تابع درجه دوم $f(x) = (a + 1){x^2} + ax + a - 1$، ریشه‌ی مضاعف دارد؟
1 )
$ \pm \frac{2}{3}$
2 )
$ \pm \frac{1}{3}$
3 )
$ \pm \frac{{\sqrt 3 }}{3}$
$ \pm \frac{{2\sqrt 3 }}{3}$
پاسخ تشریحی :
تحلیل ویدئویی تست
مرضیه موثقی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...