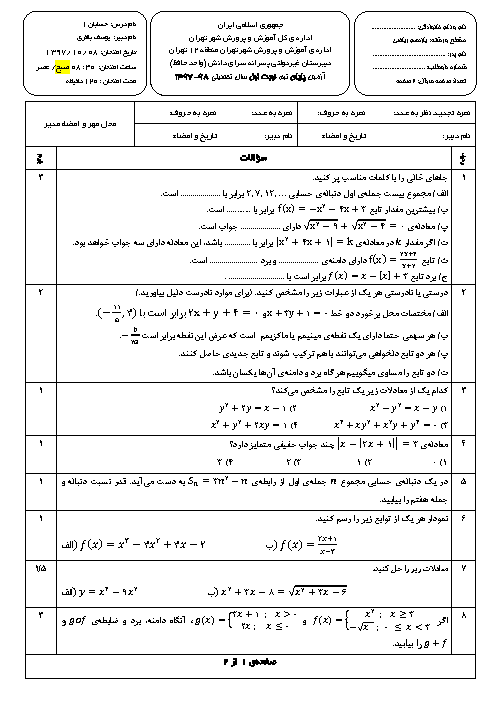
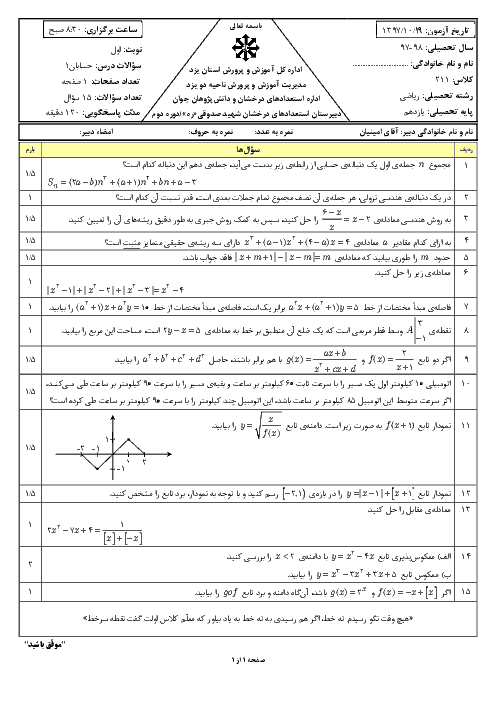
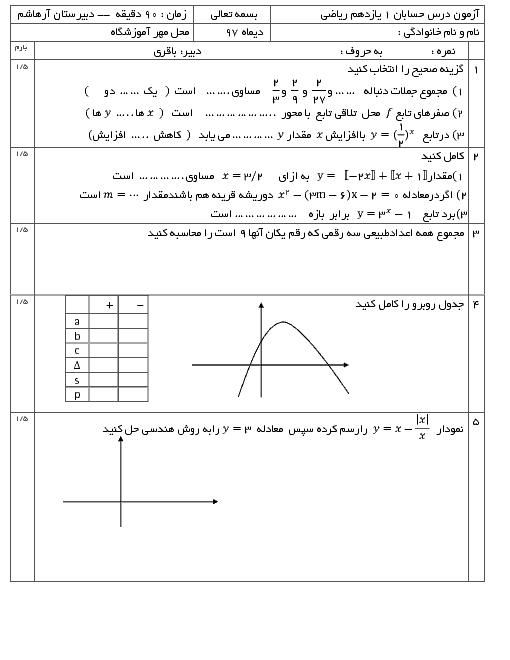
درس 1: مجموع جملات دنباله‌های حسابی و هندسی
حسابان (1)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
مجموع ده جملۀ اول دنبالۀ هندسی $\frac{1}{8},x,y,-1,...$ کدام است؟
1 )
$\frac{-511}{12}$
2 )
$\frac{-511}{24}$
3 )
$\frac{-1023}{12}$
$\frac{-1023}{24}$
پاسخ تشریحی :
تحلیل ویدئویی تست
علی شویعی نژاد 
علیرضا زینی وند 
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...