هر دو ادعا را در صورت امکان اثبات یا با استفاده از مثال نقض رد می‌کنیم.

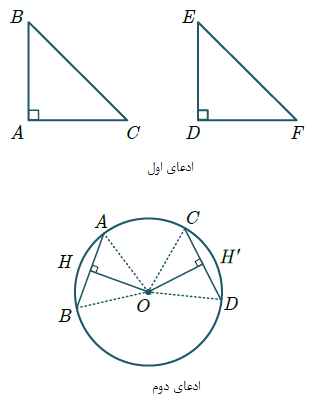
ادعای اول:

دو مثلث دلخواه ABC و DEF قائم‌الزاویه متساوی‌ الساقین هستند که هر دو وترهای برابر دارند.

$\overline {BC}  = \overline {EF}  = x$

از طرفی $\overline {AB}  = \overline {AC}  = y$ و $\overline {DE}  = \overline {DF}  = z$ در هر مثلث قائم‌الزاویه داریم.

$\begin{array}{*{20}{c}}
  {A{B^2} + A{C^2} = B{C^2}} \\ 
  {{y^2} + {y^2} = {x^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,} 
\end{array}\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}{c}}
  {D{E^2} + D{F^2} = E{F^2}} \\ 
  {{z^2} + {z^2} = {x^2}} 
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}
  {2{y^2} - {x^2}} \\ 
  {2{z^2} = {x^2}} 
\end{array} \Rightarrow {y^2} = {x^2} \Rightarrow y = z} \right.$

پس دو مثلث به حالت «:ض ض ض» هم‌نهشت هستند.

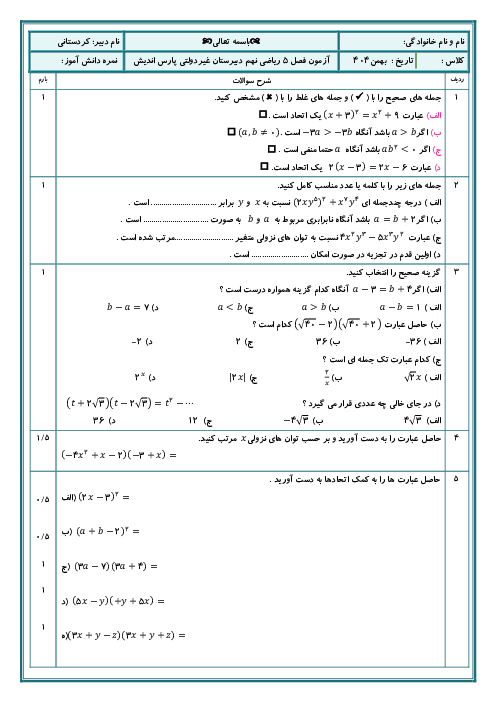
ادعای دوم:

می‌دانیم محل برخورد عمودمنصف‌های وترهای دلخواه دایره مرکز آن است.

از مرکز دایره به A و B و C و D متصل می‌کنیم، خطوط ایجاد شده شعاع‌های دایره هستند.

$OH = OH'$ :فرض

$\overline {AB}  = \overline {CD} $ :حکم

$\mathop {DHA}\limits^\Delta  \,,\,\mathop {OCH'}\limits^\Delta  \, \Rightarrow \left. {\begin{array}{*{20}{c}}
  {\overline {OA}  = \overline {OC} } \\ 
  {\overline {OH}  = {{\overline {OH} }^\prime }} 
\end{array}} \right\}\,\mathop {OHA}\limits^\Delta   \cong \mathop {OCH'}\limits^\Delta   \Rightarrow \overline {AH}  = \overline {CH'} $

به همین روش ثابت می‌کنیم $BH = DH'$ و در اینصورت:

$\begin{array}{*{20}{c}}
  {AH = CH'} \\ 
  {BH = DH'} 
\end{array}\xrightarrow{ + }AH + BH = CH' + DH' \Rightarrow \overline {AB}  = \overline {CD} $