ابتدا ضابطه‌ی $f$ را ساده‌تر می‌نويسيم:

$f(x)=\underbrace{a\operatorname{Cos}(\pi +bx)}_{-\operatorname{Cos}bx}\Rightarrow f(x)=-a\operatorname{Cos}bx$ 

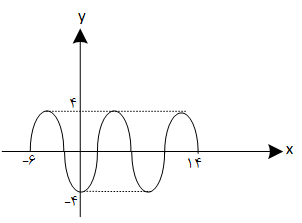
نمودار رسم شده، تابع را در $2/5$ دوره‌ی تناوب نشان می‌دهد. پس:

$\Rightarrow \frac{5}{2}T=14-(-6)\Rightarrow \frac{5}{2}T=20\Rightarrow T=8$ 

از طرفی دوره‌ی تناوب تابع از رابطه‌ی $\frac{2\pi }{\left| b \right|}$ به‌دست می‌آيد: پس: $\frac{2\pi }{\left| b \right|}=8\Rightarrow \left| b \right|=\frac{\pi }{4}$ 

از طرفی مقدار تابع در $x=0$ برابر $-4$ است، پس: $f(0)=-4\Rightarrow -a\underbrace{\operatorname{Cos}0}_{1}=-4\Rightarrow a=4$ 

در نتيجه ضابطه‌ی $f$ به‌صورت $f(x)=-4\operatorname{Cos}\frac{\pi x}{4}$ (یا $f(x)=-4\operatorname{Cos}\left( -\frac{\pi x}{4} \right)$) در آيد و داريم:

$f\left( -\frac{32}{3} \right)=-4\operatorname{Cos}\left( \frac{\pi }{4}\times \frac{-32}{3} \right)=-4\operatorname{Cos}\left( \frac{-8\pi }{3} \right)=-4\operatorname{Cos}\left( \frac{8\pi }{3} \right)=-4\operatorname{Cos}\left( 2\pi +\frac{2\pi }{3} \right)=-4\operatorname{Cos}\frac{2\pi }{3}=-4\times \frac{-1}{2}=2$  

دقت كنيد چون $\operatorname{Cos}(-\theta )=\operatorname{Cos}\theta $. جواب سؤال برای $b=-\frac{\pi }{4}$ نیز همین است.