الف)

$I=(4\times {{10}^{-3}})\sin (250\pi t)$
$\left\{ \begin{matrix}{{t}_{1}}=2ms\to I=(4\times {{10}^{-3}})\sin (250\pi \times 2\times {{10}^{-3}})\to I=(4\times {{10}^{-3}})\sin (0/5\pi )\to I=4\times {{10}^{-3}}  \\{{t}_{2}}=8ms\to I=(4\times {{10}^{-3}})\sin (250\pi \times 8\times {{10}^{-3}})\to I=(4\times {{10}^{-3}})\sin (2\pi )\to I=0  \\\end{matrix} \right.$

ب)

$\left. \begin{matrix}I={{I}_{m}}\sin (\frac{2\pi }{T}t)  \\I=(4\times {{10}^{-3}})\sin (250\pi t)  \\\end{matrix} \right\}\to \left\{ \begin{matrix}{{I}_{m}}=4\times {{10}^{-3}}  \\\frac{2\pi }{T}=250\pi   \\\end{matrix} \right.$
$\frac{2\pi }{T}=250\pi \to T=\frac{2\pi }{250\pi }\to T=0/004s\to T=4\times {{10}^{-3}}s$

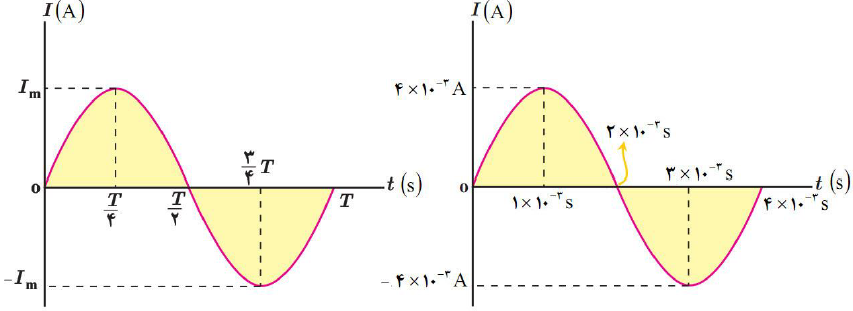
ج) با توجه به اندازه‌هایی که برای دوره و اندازه‌ی جریان بیشینه به دست آمده، نمودار جریان بر حسب زمان در یک دوره به صورت زیر می‌باشد.

${{I}_{m}}=4\times {{10}^{-3}}$
$T=4\times {{10}^{-3}}s\to \left\{ \begin{matrix}\frac{T}{4}=1\times {{10}^{-3}}s  \\\frac{T}{2}=2\times {{10}^{-3}}s  \\\frac{3T}{4}=3\times {{10}^{-3}}s  \\\end{matrix} \right.$