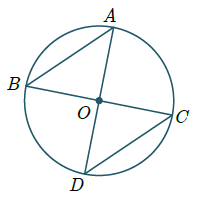
$AB = CD$ :فرض
$\overline {AB} = \overline {CD} $ :حکم
برای اثبات نقاط A و B و C و D را به مرکز دایره وصل میکنیم. در این صورت OD و OC و OB و AO شعاعهای دایره هستند.
و باهم برابرند از طرفی زوایای $A\hat OB$ و $C\hat OD$ زوایای مرکزی بوده و بهترتیب روبه دو کمالهای AB و CD هستند. طبق فرض:
$AB = CD \Rightarrow \left\{ \begin{gathered}
A\hat OB = AB \hfill \\
C\hat OD = CD \hfill \\
\end{gathered} \right. \Rightarrow A\hat OB = C\hat OD$
پس بنا به حالت ض ز ض
$\left. \begin{gathered}
AO = OC \hfill \\
A\hat OB = C\hat OD \hfill \\
OB = OD \hfill \\
\end{gathered} \right\} \Rightarrow \mathop {AOB}\limits^\Delta \simeq \mathop {COD}\limits^\Delta \Rightarrow \overline {AB} = \overline {CD} $