قسمت 5: میدان مغناطیسی حاصل از جریان الکتریکی
فیزیک (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
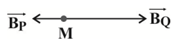
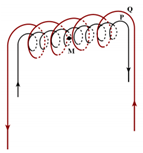
در شكل زير دو سيم‌لوله $P$ و $Q$ به طول $157cm$ طوری قرار دارند كه محور اصلی آن‌ها بر هم منطبق است. اگر جريان الكتريكی $1A$ از هر يک از سيم‌لوله‌ها بگذرد و تعداد دور سيم‌لوله‌های $P$ و $Q$ به‌ترتيب برابر 200 و 300 دور باشد، برايند ميدان‌های مغناطيسی ناشی از جريان دو سيم‌لوله در نقطهٔ $M$ روی محور اصلی مشترک دو سيم‌لوله چند تسلا است؟ $({{\mu }_{{}^\circ }}=4\pi \times {{10}^{-7}}\frac{T.m}{A},\pi =3/14)$
$8\times {{10}^{-5}}$
2 )
$24\times {{10}^{-5}}$
3 )
$16\times {{10}^{-4}}$
4 )
$4\times {{10}^{-4}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...