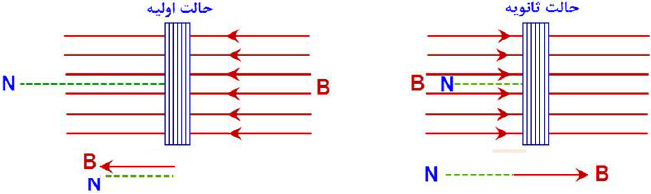
پیچه‌ای دارای 1000 حلقه است و سطح حلقه‌های آن عمود بر میدان مغناطیسی یکنواختی که اندازه آن 0/04T و جهت آن از راست به چپ است، است. میدان مغناطیسی در مدت، 0/01s تغییر…

گاما رو نصب کن!

درحال دریافت اطلاعات ...

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

** فصل 3: مغناطیس و القای الکترومغناطیسی فیزیک (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

پیچه‌ای دارای 1000 حلقه است و سطح حلقه‌های آن عمود بر میدان مغناطیسی یکنواختی که اندازه آن 0/04T و جهت آن از راست به چپ است، است. میدان مغناطیسی در مدت، 0/01s تغییر می‌کند و به 0/04T در خلاف جهت اولیه می‌رسد.

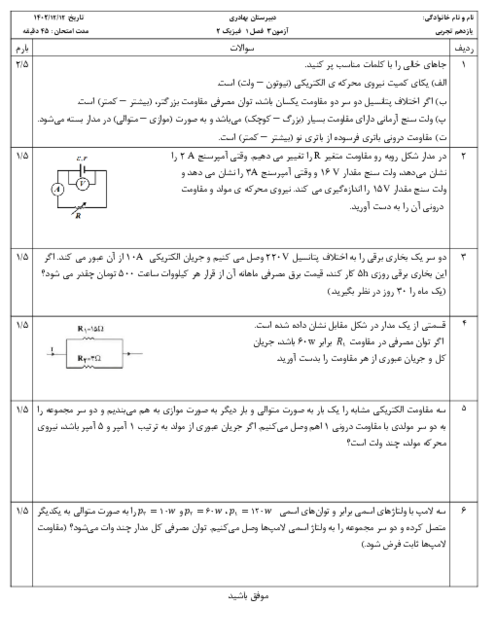
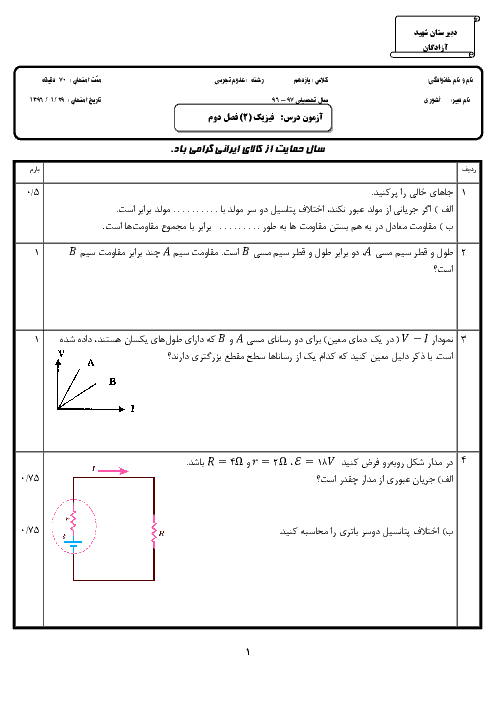
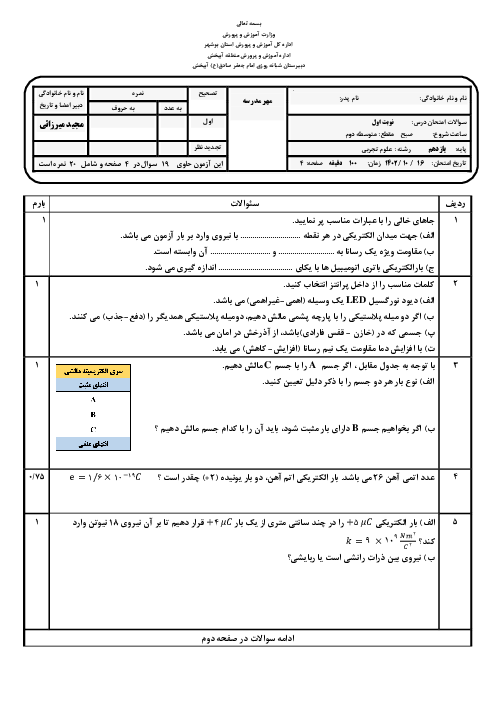
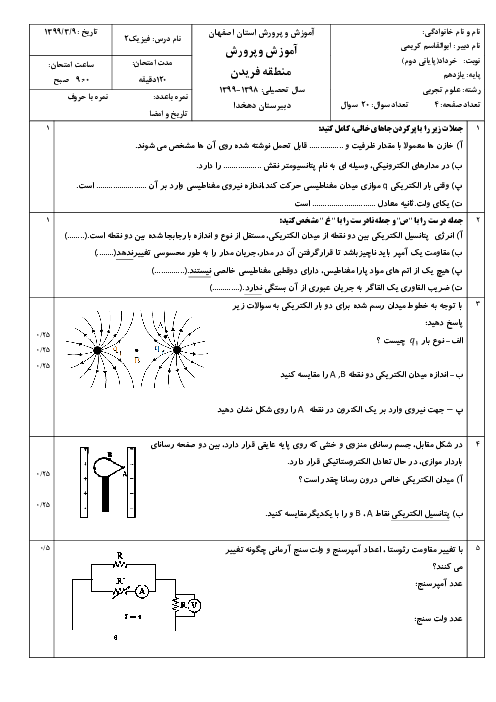
الف) اگر مساحت سطح هر حلقه‌ی پیچه $50c{{m}^{2}}$ باشد، نیروی محرکه القایی متوسط در پیچه را حساب کنید.
ب) اگر مقاومت این پیچه 100 اُهم باشد، اندازه جریان القایی را به دست آورید.

نمایش پاسخ

الف) در این مسئله می‌توان تغییرات شار مغناطیسی را ناشی از تغییر اندازه‌ی میدان مغناطیسی در نظر گرفت. میدان مغناطیسی از 0/04 تسلا در حالت اولیه به -0/04 در حالت ثانویه می‌رسد.

$\Delta \Phi ={{\Phi }_{2}}-{{\Phi }_{1}}=\left[ {{B}_{2}}-{{B}_{1}} \right]A\cos \theta $
$\Delta \Phi =(-0/04-0/04)\times (50\times {{10}^{-4}})\times \left[ \cos 0 \right]$
$\Delta \Phi =-0/08\times (50\times {{10}^{-4}})\times 1\to \Delta \Phi =-4\times {{10}^{-4}}wb$

این تغییرات شار باعث ایجاد نیروی محرکه‌ی القایی در مدار می‌شود که به صورت زیر به دست می‌آید.

$\overline{\varepsilon }=-N\frac{\Delta \Phi }{\Delta t}\to \overline{\varepsilon }=-1000\times \frac{-4\times {{10}^{-4}}}{1\times {{10}^{-2}}}\to \overline{\varepsilon }=40v$

ب)

$I=\frac{\overline{\varepsilon }}{R}\to \overline{I}=\frac{40v}{100\Omega }=0/4A$