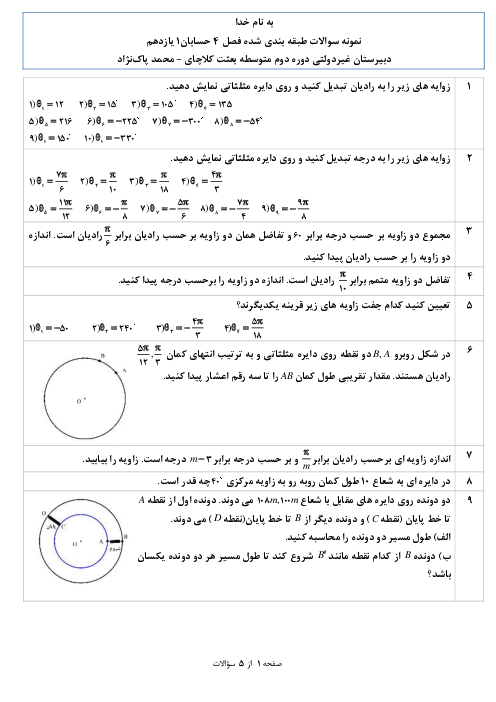
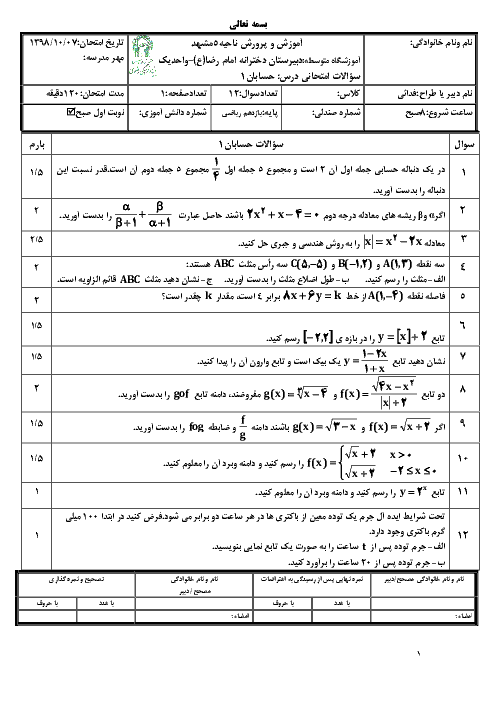
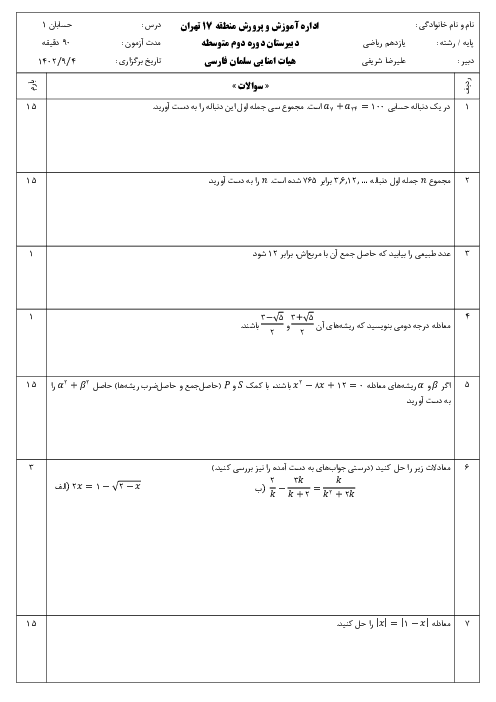
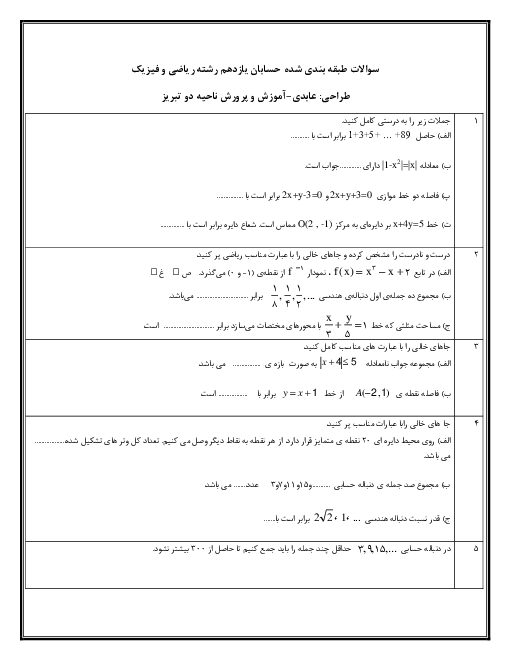
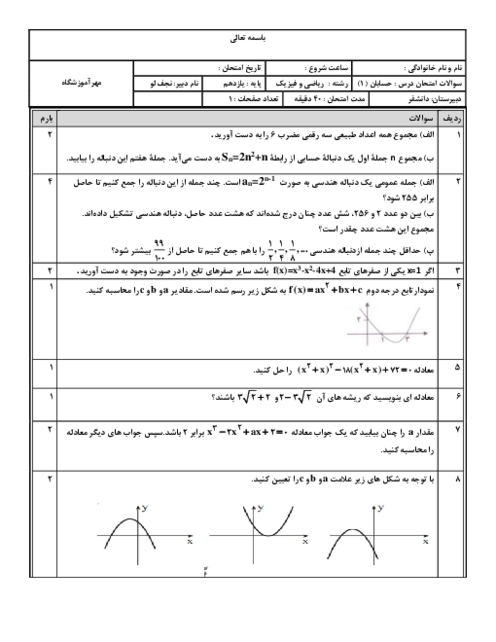
فرض کنید $tg\beta = \frac{5}{{12}},tg\alpha = \frac{3}{4}$ و $\alpha $ و $\beta $ حاده باشند، عبارتهای زیر را محاسبه کنید.
$\eqalign{
& \operatorname{Sin} (\alpha + \beta ),\operatorname{Cos} (\alpha + \beta ),\operatorname{Sin} (\alpha - \beta ) \cr
& {\operatorname{Cos} ^2}\alpha = \frac{1}{{1 + t{g^2}\alpha }} = \frac{1}{{1 + \frac{9}{{16}}}} = \frac{{16}}{{25}} \to \operatorname{Cos} \alpha = \frac{4}{5} \to \operatorname{Sin} \alpha = \frac{3}{5} \cr} $
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...