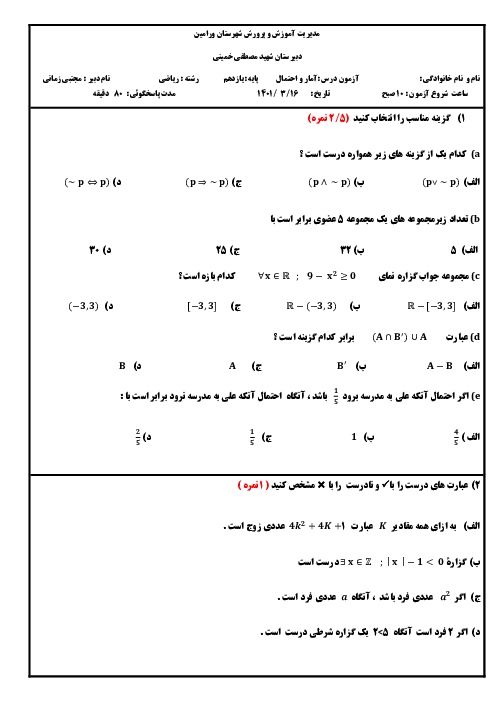
در $25$ بار پرتاب یک سکه، $9$ بار سکه «رو» آمده است. در سطح اطمینان $95$ درصد، دقیق‌ترین بازه‌ای که نسبت «رو» آمدن این سکه را نشان می‌دهد، کدام است؟
1 )
$(\frac{4}{25},\frac{14}{25})$
2 )
$(\frac{6}{25},\frac{12}{25})$
$(\frac{21}{125},\frac{69}{125})$
4 )
$(\frac{33}{125},\frac{57}{125})$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...