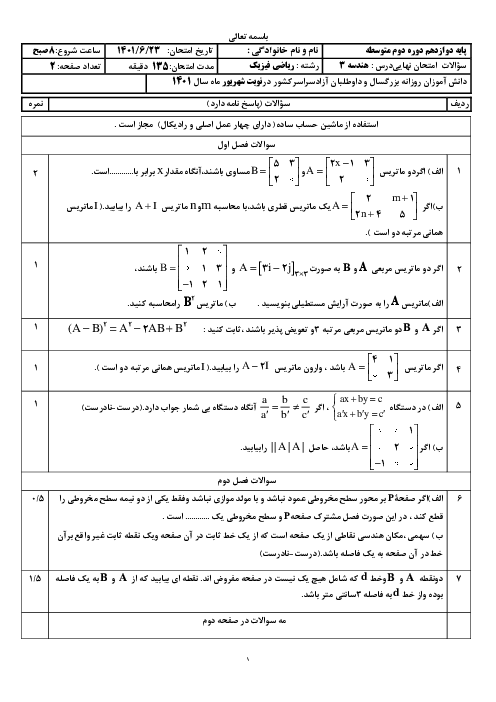
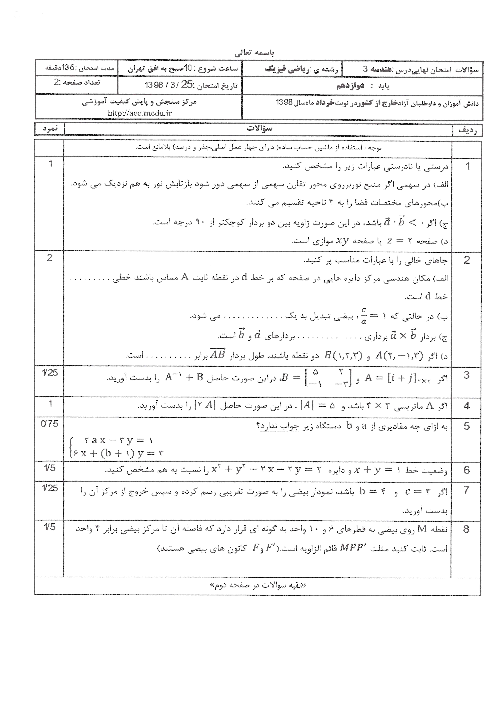
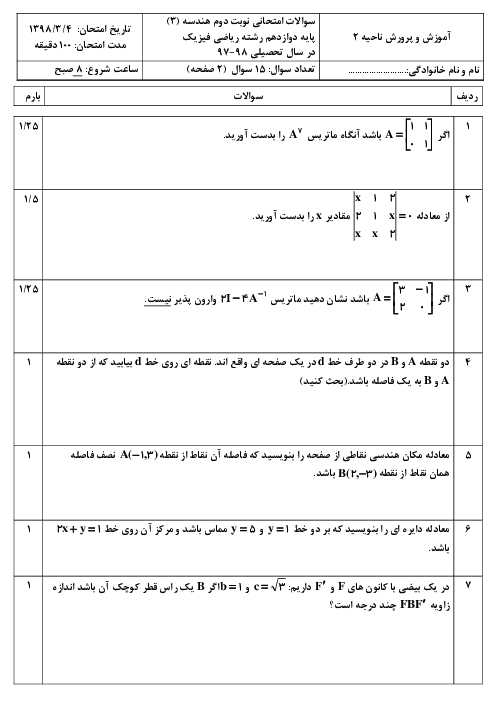
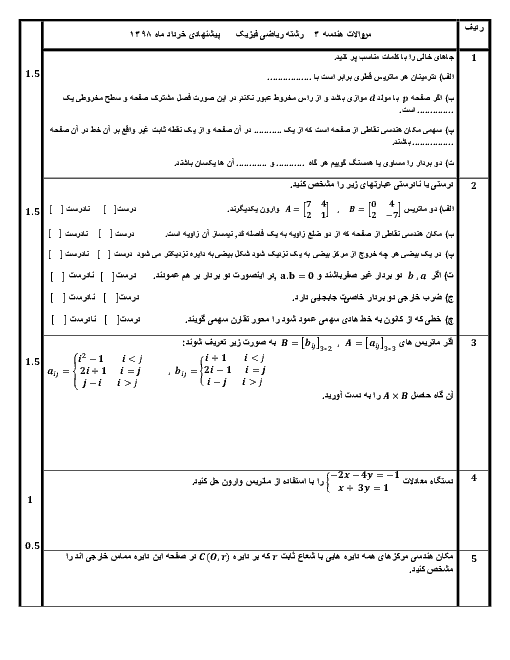
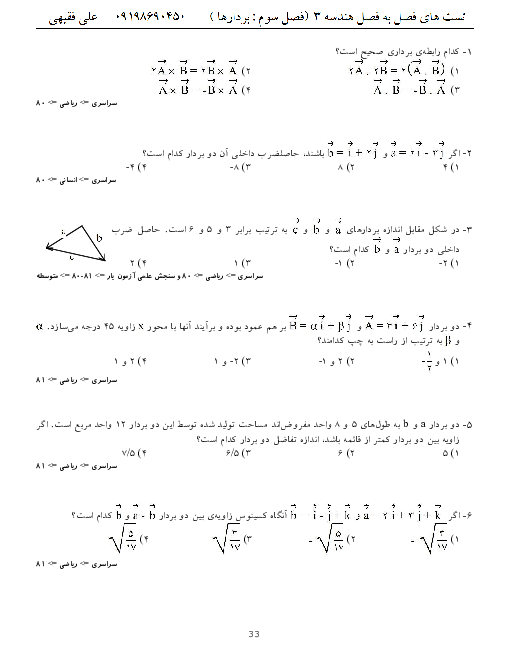
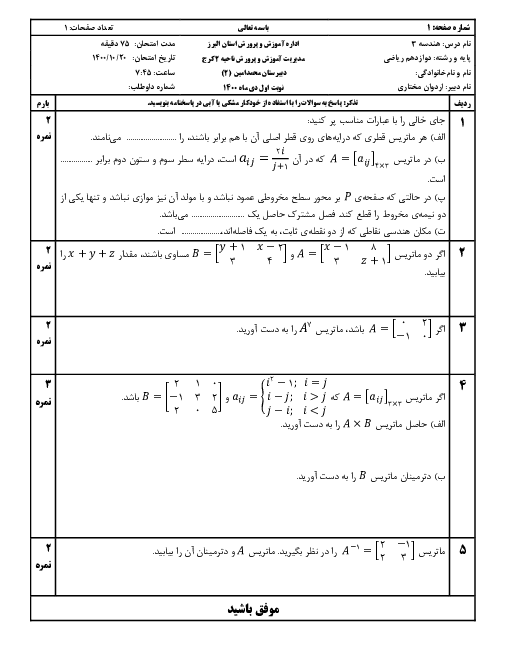
درایه‌های ${{d}_{23}}$ و ${{d}_{32}}$ را به دست آورده و مساوی هم قرار می‌دهیم تا $x$ معلوم شود:

$\left\{ \begin{matrix}    {{d}_{23}}=\left[ \begin{matrix}    1 & 1 & 1  \\ \end{matrix} \right]\left[ \begin{matrix}    3 & 1 & 0  \\    1 & 0 & 2  \\    0 & 1 & 0  \\ \end{matrix} \right]\left[ \begin{matrix}    x  \\    1  \\    x  \\ \end{matrix} \right]=\left[ \begin{matrix}    4 & 2 & 2  \\ \end{matrix} \right]\left[ \begin{matrix}    x  \\    1  \\    x  \\ \end{matrix} \right]=4x+2+2x=6x+2  \\    {{d}_{32}}=\left[ \begin{matrix}    0 & 1 & 2  \\ \end{matrix} \right]\left[ \begin{matrix}    3 & 1 & 0  \\    1 & 0 & 2  \\    0 & 1 & 0  \\ \end{matrix} \right]\left[ \begin{matrix}    1  \\    -1  \\    x  \\ \end{matrix} \right]=\left[ \begin{matrix}    1 & 2 & 2  \\ \end{matrix} \right]\left[ \begin{matrix}    1  \\    -1  \\    x  \\ \end{matrix} \right]=1+(-2)+2x=2x-1  \\ \end{matrix} \right.\Rightarrow 6x+2=2x-1\Rightarrow 4x=-3\Rightarrow x=-\frac{3}{4}$