قسمت 3: حرکت با شتاب ثابت
فیزیک (3) تجربی
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
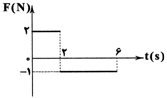
متحرکی به جرم $0/5kg$ در لحظه‌ی ${{t}_{{}^\circ }}=0$ با سرعت $2\frac{m}{s}$ در خلاف جهت محور $x$ در حال حرکت است. اگر نمودار نیروی خالص افقی وارد بر متحرک برحسب زمان مطابق شکل زیر باشد، سرعت متحرک در لحظه‌ی $t=6s$ برحسب متر بر ثانیه کدام است؟
1 )
2، در جهت محور $x$
2، در خلاف جهت محور $x$
3 )
6، در جهت محور $x$
4 )
6، در خلاف جهت محور $x$
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...