دو جعبه سیب داریم. می‌دانیم 81 درصد سیب‌های جعبۀ اول و 90 درصد سیب‌های جعبۀ دوم سالم هستند. به تصادف 4 سیب از جعبۀ اول و 5 سیب از جعبۀ دوم خارج کرده و در یک کیسه…

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 7: احتمال ریاضی (3) دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

دو جعبه سیب داریم. می‌دانیم 81 درصد سیب‌های جعبۀ اول و 90 درصد سیب‌های جعبۀ دوم سالم هستند. به تصادف 4 سیب از جعبۀ اول و 5 سیب از جعبۀ دوم خارج کرده و در یک کیسه می‌ریزیم و سپس به تصادف از کیسه سیبی خارج می‌کنیم. احتمال این‌که سیب خارج‌شده ناسالم باشد کدام است؟

1 )

0/14

2 )

0/16

3 )

0/18

4 )

0/2

نمایش پاسخ

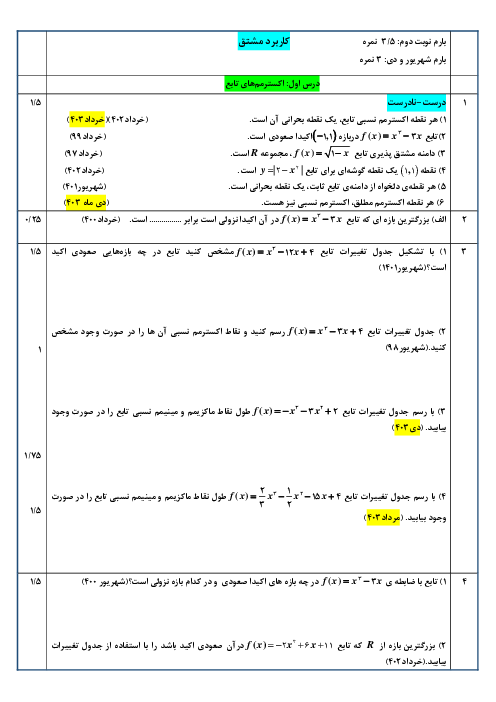
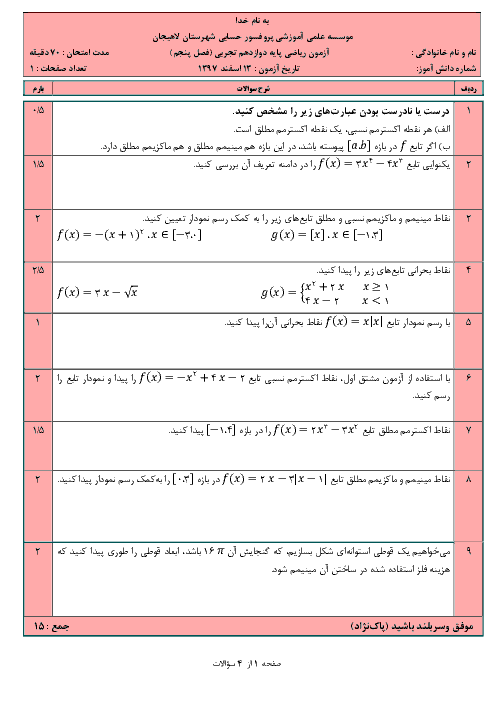
نکته: اگر فرض کنیم در حالت کلی ${A_n},...{A_2},{A_1}$ پیشامدهایی باشند که بر روی فضای نمونه‌ای S یک افزار تشکیل داده باشند و B یک پیشامد دلخواه باشد، رابطۀ زیر حاصل خواهد شد که به آن قانون احتمال کل می‌گوییم:

$P(B) = \sum\limits_{i = 1}^n {P(B \cap {A_1}) = \sum\limits_{i = 1}^n {P({A_i})P(B\left| {{A_i})} \right.} } $

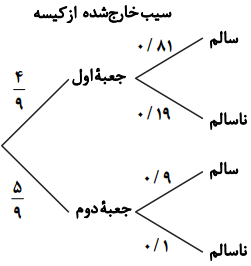
در کیسه‌ای 4 سیب از جعبۀ اول و 5 سیب از جعبۀ دوم وجود دارد، پس احتمال آن‌که سیب خارج‌شده از کیسه، مربوط به جعبۀ اول باشد برابر $\frac{4}{9}$ و احتمال این‌که مربوط به جعبۀ دوم باشد، برابر $\frac{5}{9}$ است.

بنابراین احتمال آن‌که سیب خارج شده از کیسه ناسالم باشد، برابر است با:

$P = \frac{4}{9} \times 0/19 + \frac{5}{9} \times 0/1 = \frac{{76}}{{900}} + \frac{5}{{90}} = \frac{{126}}{{900}} = \frac{{14}}{{100}} = 0/14$