درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
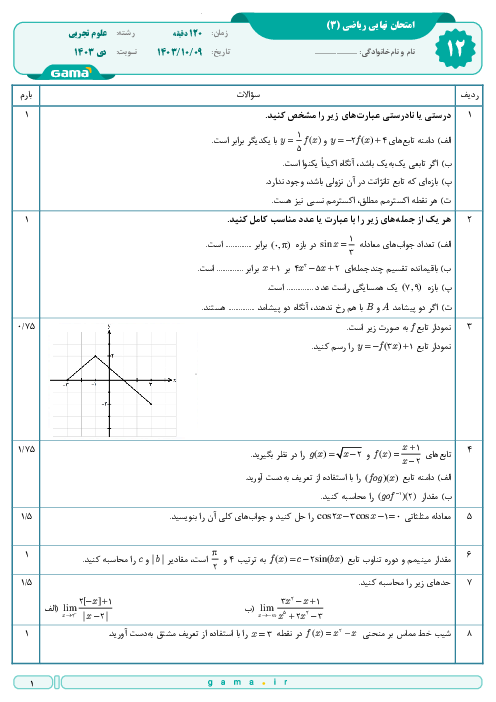
اگر تابع $f$ نزولی و دامنهٔ آن $\mathbb{R}$ باشد، دامنهٔ تابع $y=\sqrt{f(2)-f(\left| x-1 \right|)}$ کدام است؟
1 )
$\left( -\infty ,-3 \right]\bigcup \left[ 1,+\infty \right)$
2 )
$\left[ -1,3 \right]$
$\left( -\infty ,-1 \right]\bigcup \left[ 3,+\infty \right)$
4 )
$\mathbb{R}$
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...