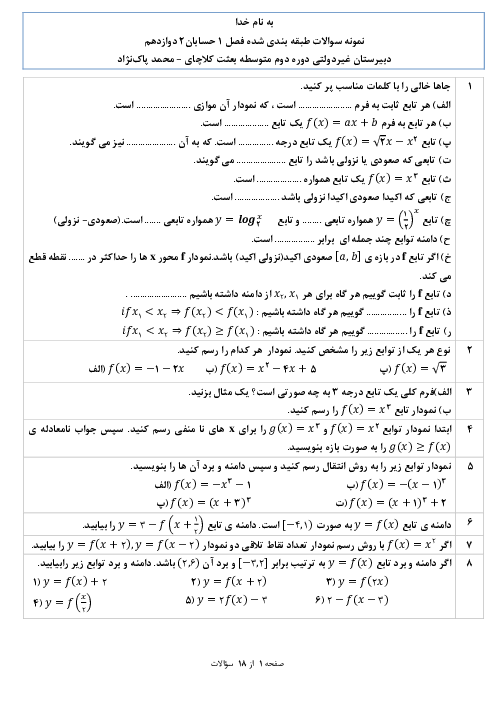
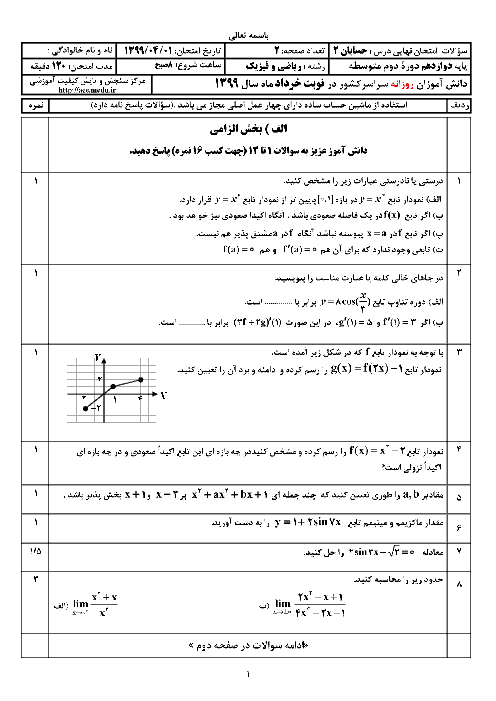
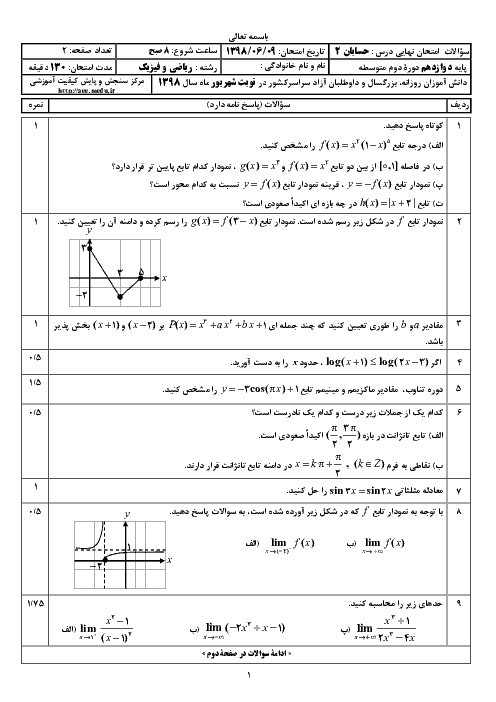
درس 1: اکسترممهای یک تابع و توابع صعودی و نزولی
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
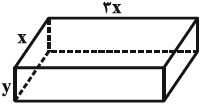
میخواهيم با يك قطعه سيم به طول $48$ واحد، يك مكعب مستطيل بسازيم. بيشترين حجم اين مكعب مستطيل، در صورتیکه كه يكی از بعدها $3$ برابر بعد ديگر باشد، كدام است؟