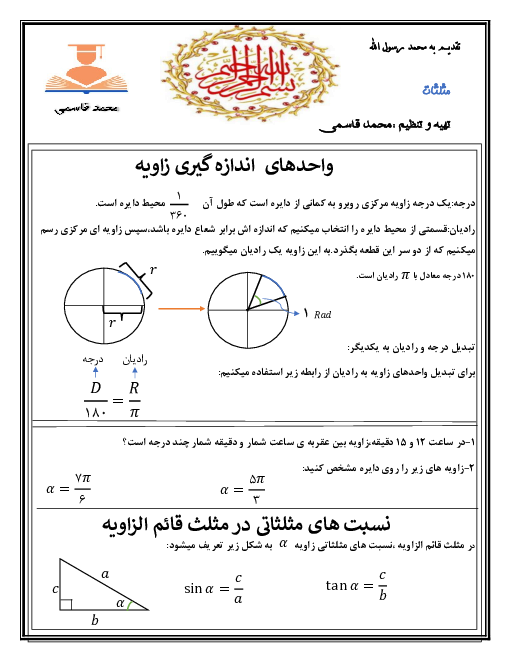
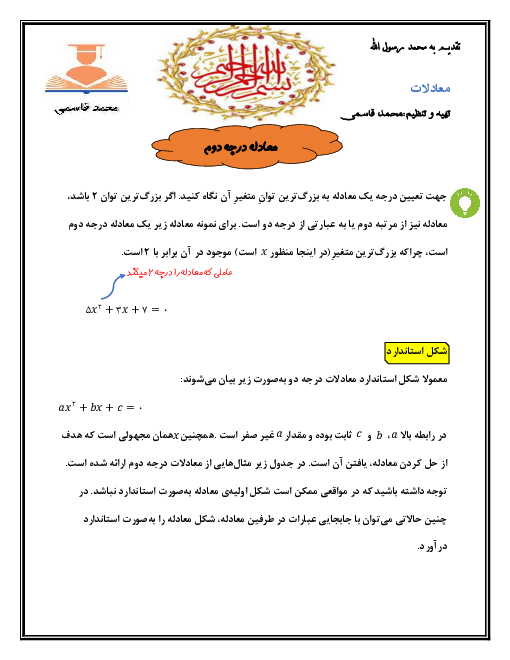
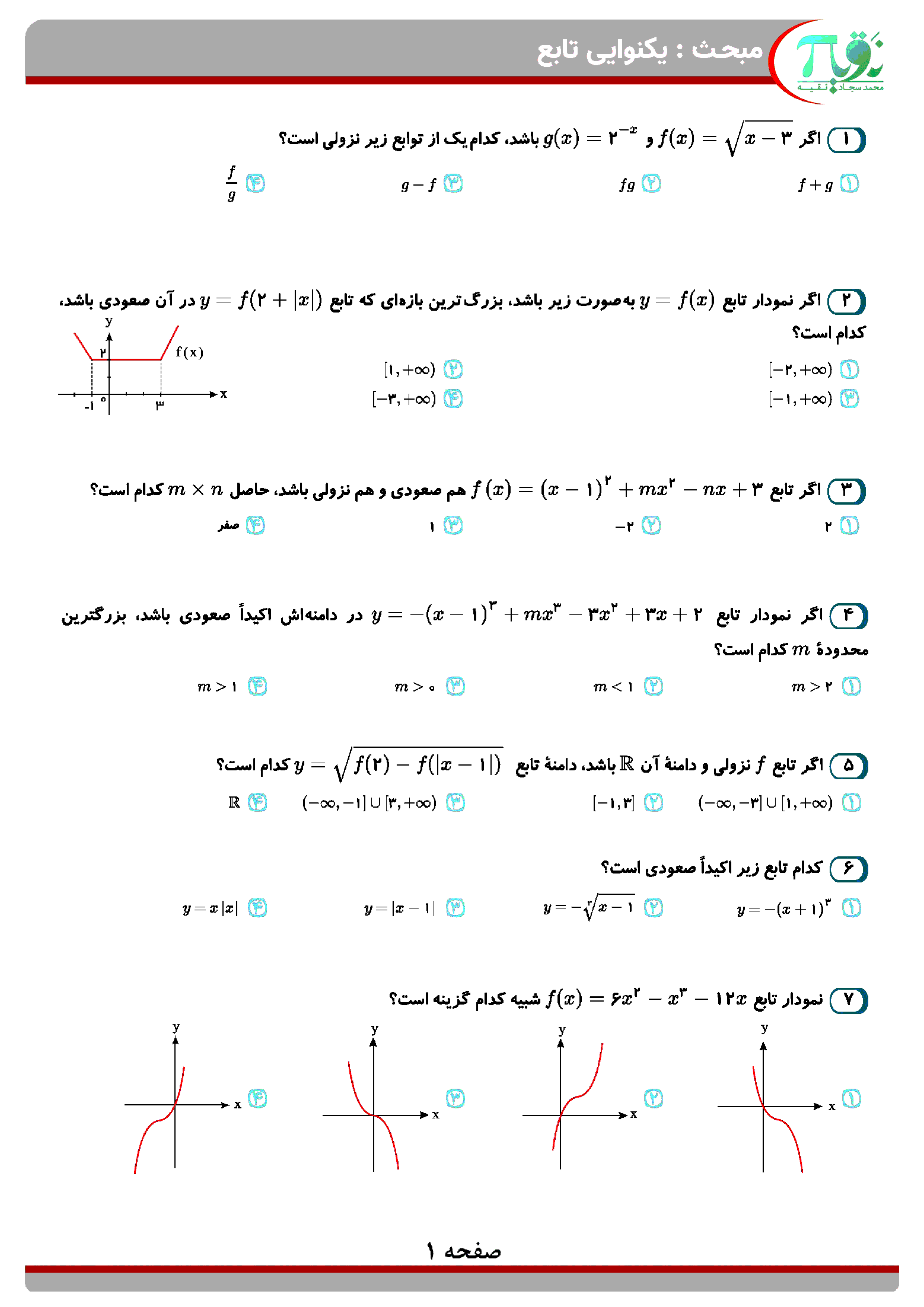
یک دایره به شعاع 2، داخل ذوزنقه متساوی‌الساقینی محاط شده است. اگر یکی از زوایای ذوزنقه 60 درجه باشد، مساحت این ذوزنقه کدام است؟
1 )
$\frac{{12}}{{\sqrt 3 }}$
2 )
$\frac{{16}}{{\sqrt 3 }}$
3 )
$\frac{{24}}{{\sqrt 3 }}$
$\frac{{32}}{{\sqrt 3 }}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...