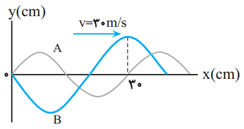
در ابتدا با استفاده از شكل داده شده در سوال، موج هر يک از موج‌ها را به‌دست می‌آوريم و سپس با استفاده از رابطهٔ $\lambda =vT$ دورهٔ تناوب آن‌ها را حساب می‌كنيم: 

برای موج $B$ $\Rightarrow \left\{ \begin{matrix} \frac{3{{\lambda }_{B}}}{4}=30\Rightarrow {{\lambda }_{B}}=40cm=0/4m  \\ v=30\frac{m}{s}  \\ \end{matrix} \right.$

${{T}_{B}}=\frac{1}{{{f}_{B}}}=\frac{{{\lambda }_{B}}}{v}=\frac{0/4}{30}=\frac{4}{300}\Rightarrow {{T}_{B}}=\frac{1}{75}s$

برای موج $A$ $\Rightarrow \left\{ \begin{matrix} {{\lambda }_{A}}=30cm=0/3m  \\ v=30\frac{m}{s}  \\ \end{matrix} \right.$

${{T}_{A}}=\frac{1}{{{f}_{A}}}=\frac{{{\lambda }_{A}}}{v}=\frac{0/3}{30}=\frac{3}{300}\Rightarrow {{T}_{A}}=\frac{1}{100}s$

اكنون با استفاده از رابطهٔ $T=\frac{t}{n}$، تعداد نوسان‌های چشمهٔ موج هر يک از موج‌ها را به‌دست می‌آوريم: 

${{n}_{B}}=\frac{t}{{{T}_{B}}}\xrightarrow[{{T}_{B}}=\frac{1}{75}s]{t=20s}{{n}_{B}}=\frac{20}{\frac{1}{75}}\Rightarrow {{n}_{B}}=1500$

${{n}_{A}}=\frac{t}{{{T}_{A}}}\xrightarrow[{{T}_{A}}=\frac{1}{100}s]{t=20s}{{n}_{A}}=\frac{20}{\frac{1}{100}}\Rightarrow {{n}_{A}}=2000$

اختلاف تعداد نوسان‌ها در مدت $20s$ برابر است با:

$\Delta n={{n}_{A}}-{{n}_{B}}=2000-1500\Rightarrow \Delta n=500$