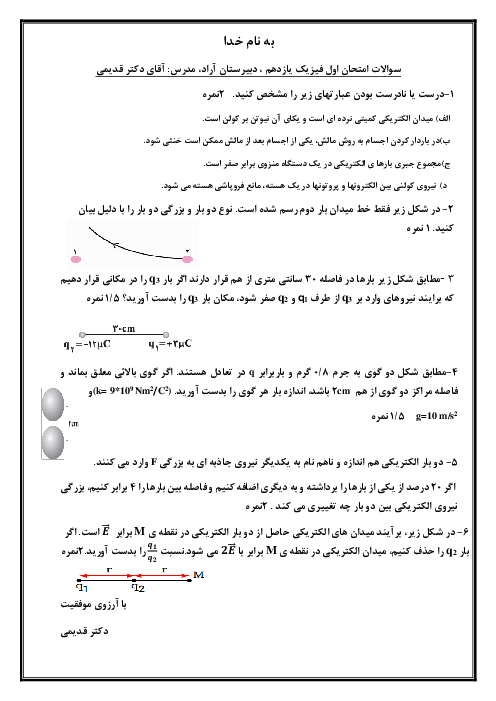
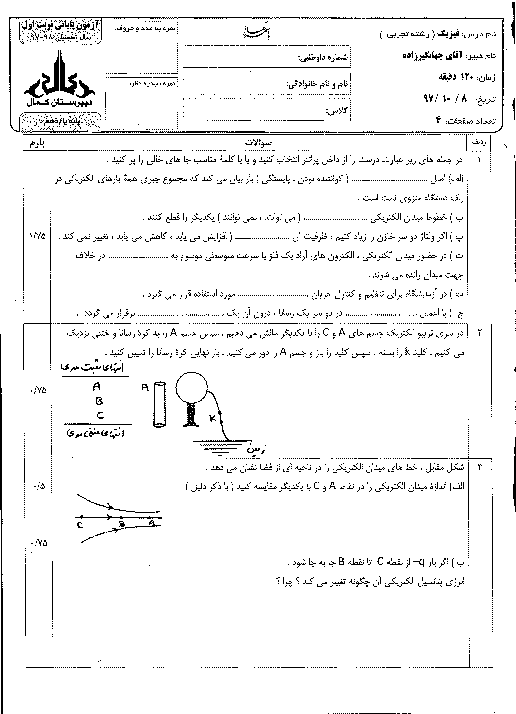
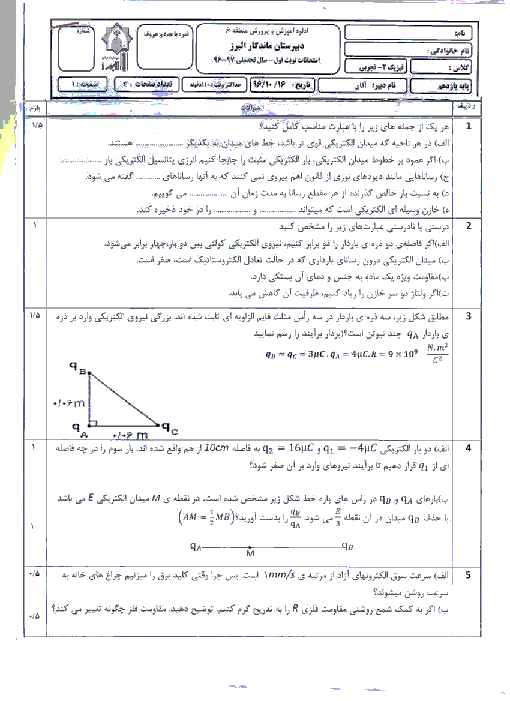
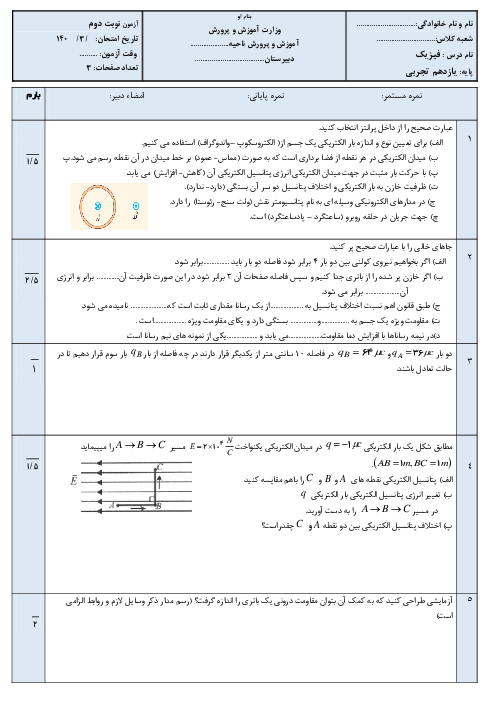
در شکل زیر دایره و مربع هممرکز هستند و بر روی هریک 4 بار هماندازه به فاصلههای مساوی از یکدیگر قرار دارند. اگر شعاع دایره برابر با 60cm، اندازهٔ هر ضلع مربع برابر با 40cm و اندازهٔ هر بار $4\mu C$ باشد، میدان الکتریکی برآیند در نقطهٔ O در SI کدام است؟ $(k=9\times {{10}^{9}}\frac{N.{{m}^{2}}}{{{C}^{2}}})$
1 )
$20\times {{10}^{5}}\overrightarrow{i}-18\times {{10}^{5}}\overrightarrow{j}$
$-16\times {{10}^{5}}\overrightarrow{i}-18\times {{10}^{5}}\overrightarrow{j}$
3 )
$-20\times {{10}^{5}}\overrightarrow{i}-18\times {{10}^{5}}\overrightarrow{j}$
4 )
$16\times {{10}^{5}}\overrightarrow{i}+18\times {{10}^{5}}\overrightarrow{j}$
پاسخ تشریحی :