فصل 3: حد بینهایت و حد در بینهایت
ریاضی (3)
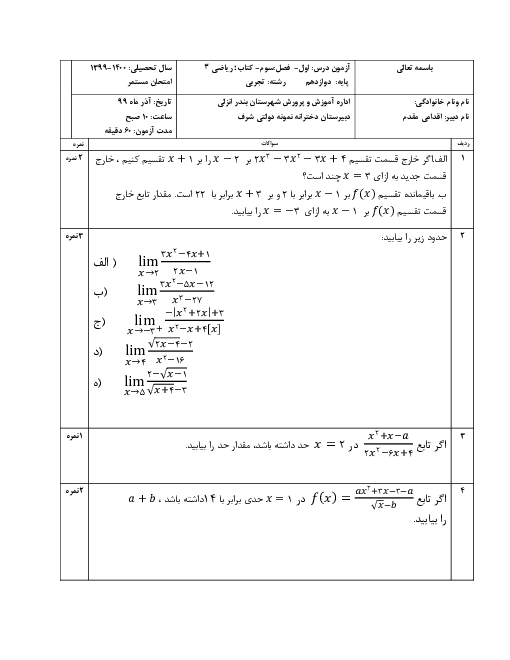
دوازدهم
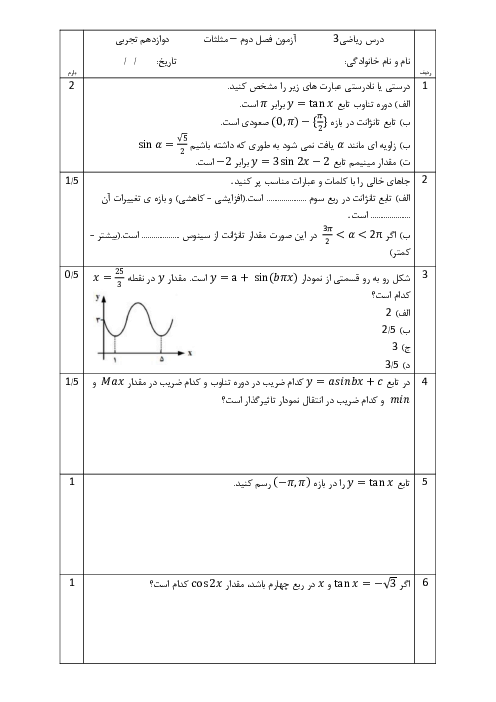
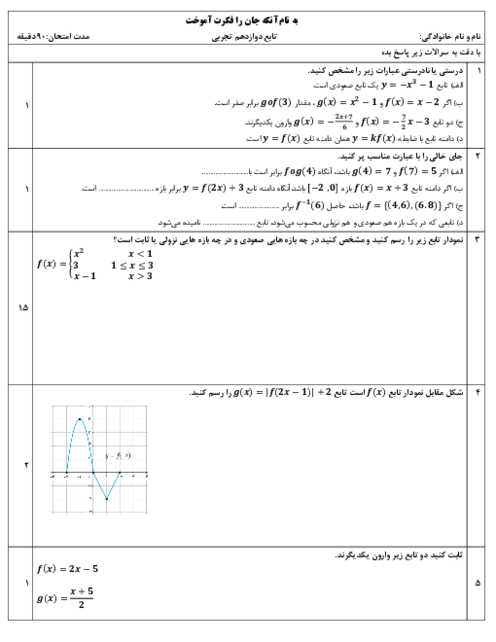
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
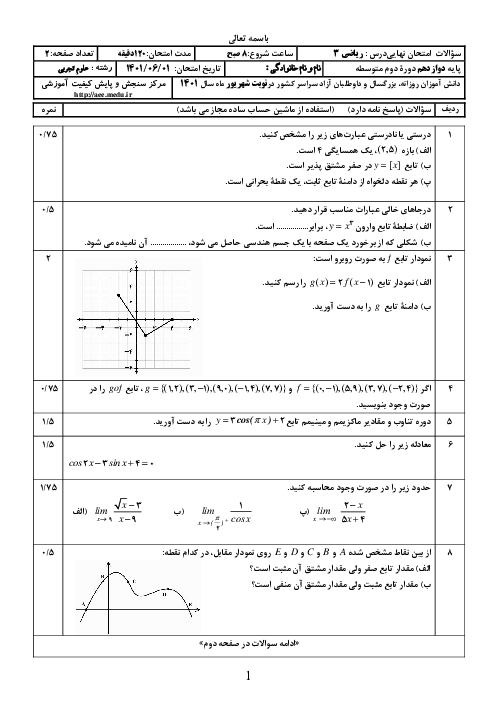
چند جملهای $p(x) = {x^{3n + 1}} + 2{x^{3n}} + {x^6} + 3{x^5} + 16a$ به ازای هر عدد طبیعی $a$ بر $x + 2$ بخشپذیر است. برای $n = 1$ ، باقیمانده تقسیم $p(x)$ بر ${x^2} + 2x - 3$ کدام است؟