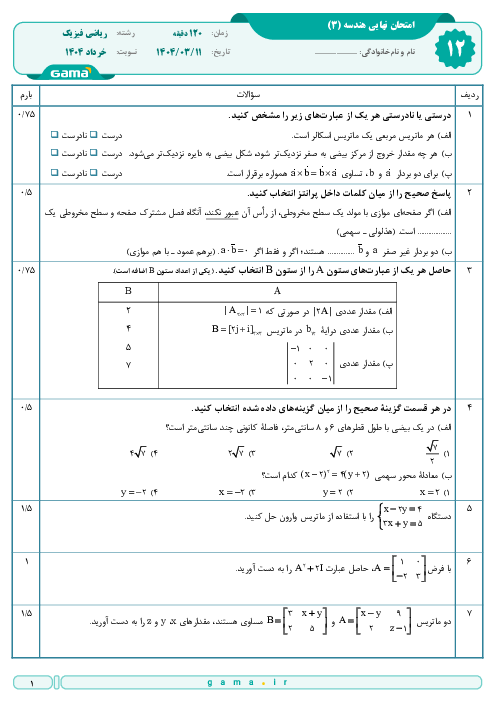
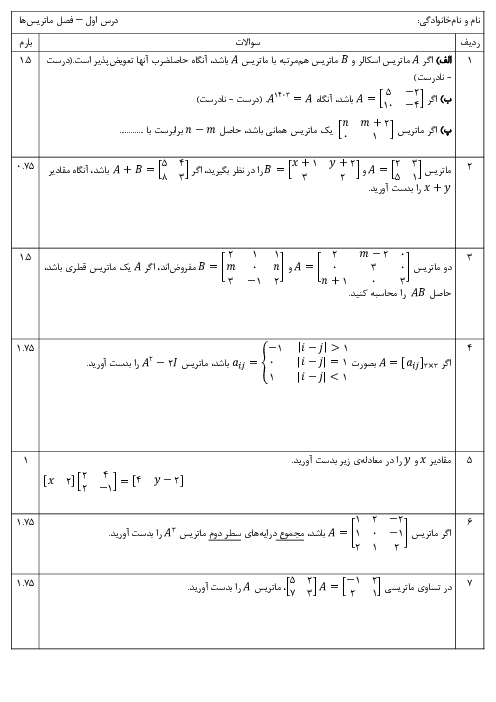
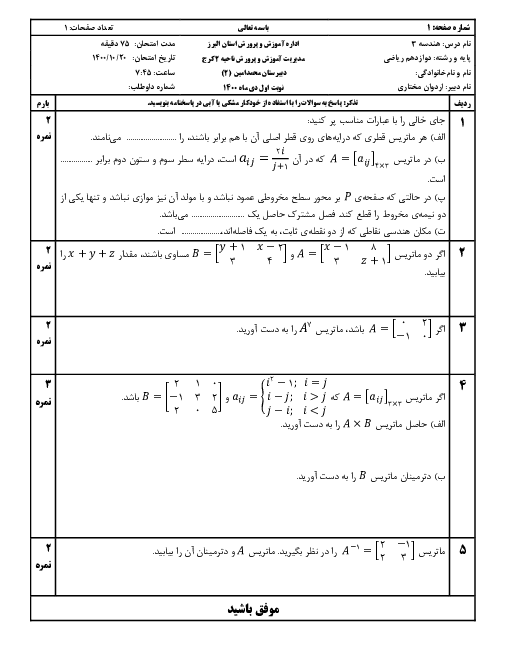
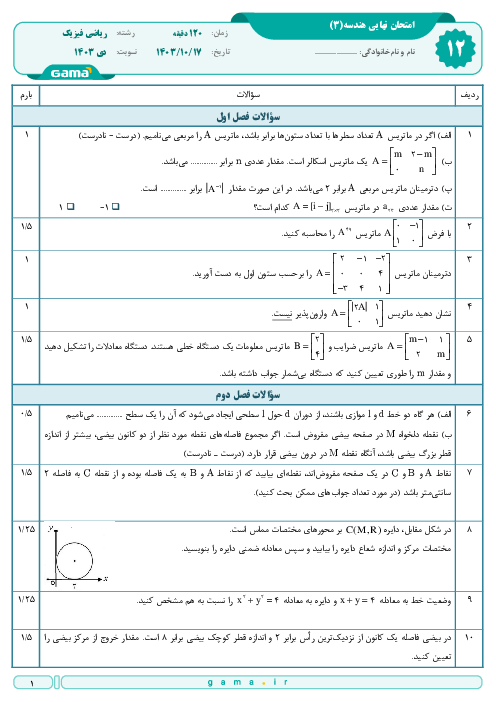
نکته: اگر ${{A}_{m\times p}}\times {{B}_{p\times n}}={{C}_{m\times n}}$، آنگاه درایهٔ ${{c}_{ij}}$ در ماتریس $C$، اط ضرب سطر $i$اُم $A$ در ستون $j$اُم $B$ به‌دست می‌آید.

نکته: ماتریس قطری، ماتریسی مربعی است که تمام درایه‌های غیر واقع بر قطر اصلی آن، صفر هستند.

$A\times B=\left[ \begin{matrix} \begin{matrix} 2x & 1  \\ \end{matrix}  \\ \begin{matrix} -1 & y  \\ \end{matrix}  \\ \end{matrix} \right]\times \left[ \begin{matrix} \begin{matrix} 1  \\ -1  \\ \end{matrix} & \begin{matrix} 1  \\ 2  \\ \end{matrix}  \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} 2x-1  \\ -1-y  \\ \end{matrix} & \begin{matrix} 2x+2  \\ -1+2y  \\ \end{matrix}  \\ \end{matrix} \right]$

 بايد درايه‌های غيرواقع بر قطر اصلی برابر صفر باشند، پس:

$\left\{ \begin{matrix} 2x+2=0\Rightarrow x=-1  \\ -1-y=0\Rightarrow y=-1  \\ \end{matrix} \right.$

 بنابراين مجموع درايه‌های ماتريس $A\times B=\left[ \begin{matrix} \begin{matrix} -3 & 0  \\ \end{matrix}  \\ \begin{matrix} 0 & -3  \\ \end{matrix}  \\ \end{matrix} \right]$ برابر است با: $-3+(-3)=-6$