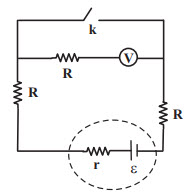
در حالتی كه كليد بسته است، دو سر شاخه‌ای از مدار كه ولت‌سنج ايده‌آل در آن قرار دارد، اتصال كوتاه می‌شود و در نتيجه المان‌های آن شاخه از مدار حذف می‌شوند. پس مقاومت خارجی مدار در اين حالت برابر با ${{R}_{eq}}=R+R=2R$ می‌شود. از طرفی توان مفید مولد از رابطهٔ $P=IV=\varepsilon I-r{{I}^{2}}$ به‌دست می‌آید که یک تابع درجهٔ دوم بر حسب $I$ است. بیشینهٔ این تابع به‌ازای $I=-\frac{b}{2a}=\frac{\varepsilon }{2r}$ به‌دست می‌آید. از مقایسهٔ $I=\frac{\varepsilon }{2r}$ و $I=\frac{\varepsilon }{{{R}_{eq}}+r}$، نتیجه می‌گیریم:

${{R}_{eq}}=r\xrightarrow{{{R}_{eq}}=2R}r=2R$

در حالتی كه كليد باز است، ولت‌سنج به طور متوالی در شاخهٔ اصلی مدار بسته شده است. چون ولت‌سنج ايده‌ال دارای مقاومت بسيار بالا است، $I=0$ و $P=\varepsilon I-r{{I}^{2}}=0$ می‌شود.