تابع از نظر پیوستگی در و چگونه است؟ | ریاضی (2) یازدهم شماره 60121

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

گام به گام نوبت اول کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

تعداد مشاهده رایگان باقی مانده: 5 صفحه

درس 3: پیوستگی ریاضی (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

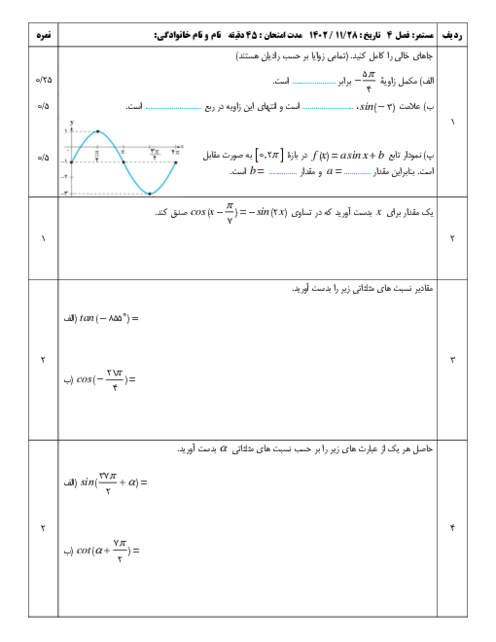
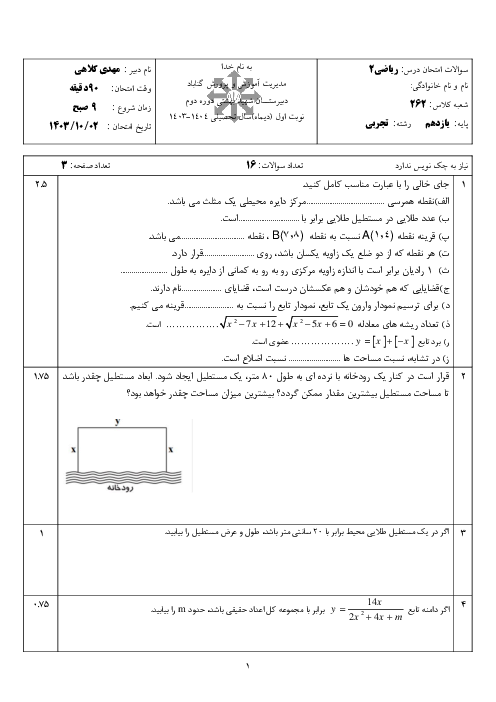
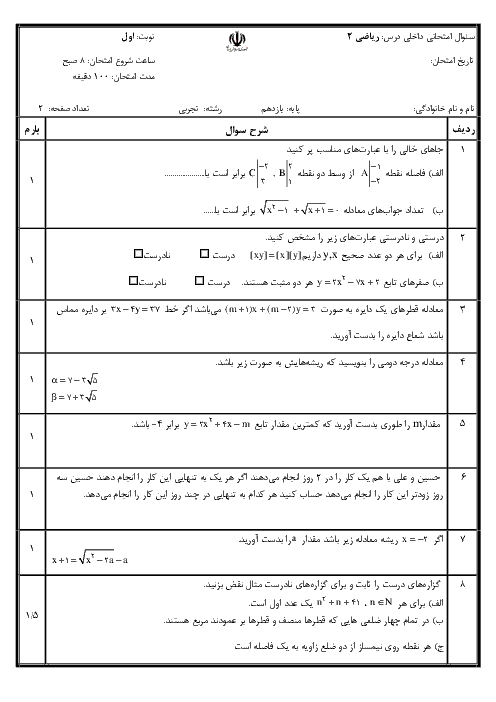
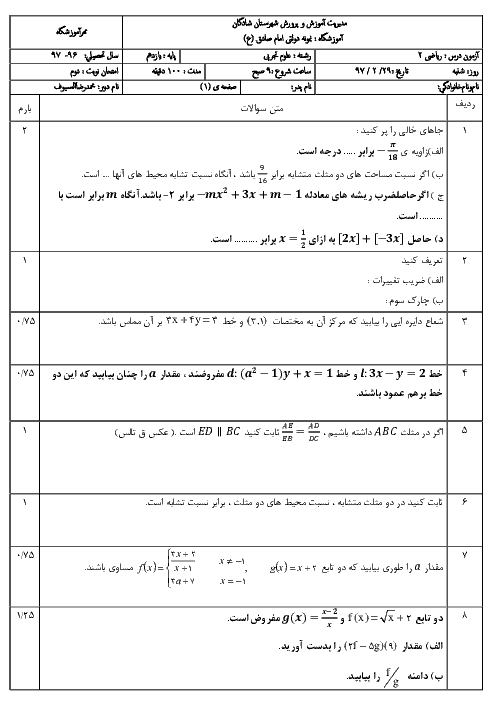
تابع $f(x)=\left\{ \begin{matrix} \left[ -2x \right],x\lt -3 \\ -2x-1,-3\le x\lt 4 \\ -\frac{{{x}^{2}}}{2}-\frac{x}{4},x\gt 4 \\ \end{matrix} \right.$ از نظر پیوستگی در $x=-3$ و $x=4$ چگونه است؟

1 )

در 3- پیوسته، در 4 ناپیوسته

2 )

در 3- ناپیوسته، در 4 ناپیوسته

3 )

در 3- ناپیوسته، در 4 پیوسته

4 )

در 3- پیوسته، در 4 پیوسته

نمایش پاسخ

$\left. \begin{matrix} \underset{x\to {{(-3)}^{-}}}{\mathop{\lim }}\,f(x)=\left[ -2{{(-3)}^{-}} \right]=\left[ {{6}^{+}} \right]=6 \\ \underset{x\to {{(-3)}^{+}}}{\mathop{\lim }}\,f(x)=-2(-3)-1=6-1=5 \\ \end{matrix} \right\}\Rightarrow $ حد ندارد، در نتیجه در $x=-3$ ناپیوسته است.

$f(-3)=-2(-3)-1=5$

$\underset{x\to {{4}^{-}}}{\mathop{\lim }}\,f(x)=-2(4)-1=-9$

$\underset{x\to {{4}^{+}}}{\mathop{\lim }}\,f(x)=-\frac{{{(4)}^{2}}}{2}-\frac{4}{4}=-8-1=-9$

$f(4)=$ وجود ندارد

چون $f(4)$ وجود ندارد، پس در $x=4$ هم ناپیوسته است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده