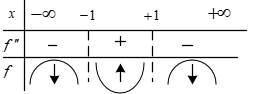
برای تعیین تقعر نمودار کافی است علامت مشتق دوم را تعیین کنیم.

در نقاط مرزی $x=-1$ و $x=1$ تابع پیوسته است. بنابراین تابع در کل دامنه‌اش یعنی $R$ پیوسته است.

 $\begin{align}
  & {f}'(x)=\left\{ \begin{matrix}
   -2x\,\,\,\,\,\,,\,\,\,\,\,\,\,x \gt 1  \\
   2x+5\,\,\,\,\,\,\,\,,\,\,\,\,\,\,-1 \lt x \lt 1  \\
   -2x+1\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,x\le -1  \\
\end{matrix} \right.\Rightarrow \left\{ \begin{matrix}
   {{{{f}'}}_{-}}(1)\ne {{{{f}'}}_{+}}(1)  \\
   {{{{f}'}}_{-}}(-1)\ne {{{{f}'}}_{+}}(-1)=3  \\
\end{matrix} \right. \\
 & {f}''(x)=\left\{ \begin{matrix}
   -2\,\,\,,\,\,\,\,\,x \gt 1  \\
   2\,\,\,,\,\,\,\,\,\,-1 \lt x \lt 1  \\
   -2\,\,\,\,,\,\,\,\,\,\,\,x<-1  \\
\end{matrix} \right. \\
\end{align}$

طبق آزمون مشتق دوم در نقاط $X=1$ و $X=-1$ تقعر عوض می‌شود اما در $X=1$ چون ${{{f}'}_{-}}(1)\ne {{{f}'}_{+}}(1)$ می‌باشد، پس $X=1$ عطف نمی‌باشد و فقط $X=-1$ عطف مایل است چون ${{{f}'}_{-}}(-1)\ne {{{f}'}_{+}}(-1)=3$ می‌باشد.